21．(本小题14分)

已知函数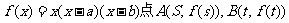

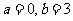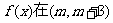(1)若，函数上既能取得极大值，又能取得极小值，求实数的取值范围.

(2)当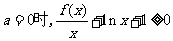对任意的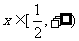恒成立，求b的取值范围.

(3)若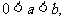函数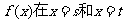处取得极值，且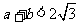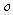，为坐标原点，证明：直线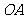与不可能垂直.

()

20．(本小题13分)

已知椭圆的中心在原点，离心率为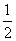，一个焦点是.

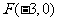　 　(1)求椭圆的方程；

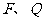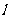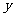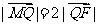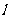　 　(2)设Q是椭圆上的一点，且过点的直线与轴交于点M.若，求直线的斜率.

19．(本小题12分)

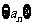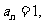已知等差数列的首项公差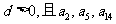恰好是等比数列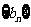的前三项

(1)求数列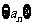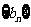，的通项公式.

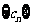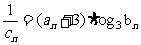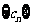(2)若数列对于任意自然数n均有，求数列的前项和.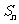

18．(本小题12分)

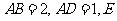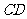如图，在矩形ABCD中，是的中点，以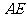为折痕，将向上折起，使D为且平面.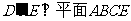

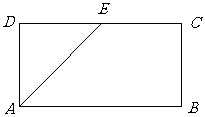
(1)证明：

(2)求二面用的大小.

(3)求四棱锥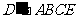的体积.

17．(本小题12分)

已知函数

(1)求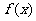的值域

(2)设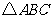的内角A.B.C的对边长分别为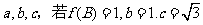，求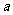

16．(本小题12分)

某工厂生产一种零件，该零件有甲.乙两项技术指标需要检验，设两项技术指标检验互不影响，经研究甲项指标合格率为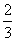，乙项指标合格率为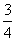.规定:两项指标都合格的零件为一等品,其中一项不合格的为二等品，两项均不合格的为次品.已知生产一个一.二等品分别获利500元，200元，出现一个次品亏损400元.

(1)求生产1个零件的利润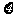的分布列；

(2)求生产1个零件的平均利润；

(3)若该厂某时段生产了5个零件，设这5个零件中一等品的个数为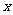，求.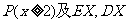

15．已知函数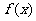满足： 　　　　　　.

14．一空间几何体的三视图(单位：cm)如图所示,则此几何体的表面积为　　　　

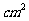
13．某人午觉醒来，发现表停了，他打开收音机，想听电台的整点报时，则他等待的时间不多于5分钟的概率为　　　　　　 .

12．已知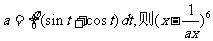展开式中的常数项为　　　　　　 .