
6. 计算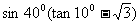 =________。
=________。
◆简答:1-4.AABA;
5. 已知α+β=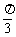 ,且
,且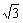 (tanαtanβ+c)+tanα=0(c为常数),那么tanβ=______
(tanαtanβ+c)+tanα=0(c为常数),那么tanβ=______
4. 已知tanα,tanβ是方程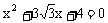 两根,且α,β
两根,且α,β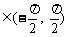 ,则α+β=( )
,则α+β=( )
A、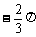 B、
B、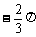 或
或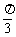 C、
C、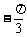 或
或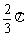 D、
D、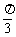 。
。
3.已知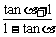 =2007,则
=2007,则 的值为
( )
的值为
( )
A、2006 B、2007 C、2009 D、2010
2.锐角三角形的内角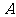 、
、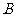 满足
满足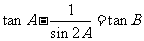 ,则有
( )
,则有
( )
A.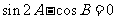 B.
B.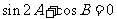
C.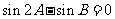 D.
D.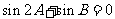
1.(2006湖北)若ΔABC的内角A满足sin2A=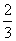 ,则sinA+cosA= ( )
,则sinA+cosA= ( )
A.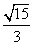 B. -
B. -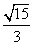 C.
C. 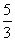 D.-
D.-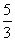
4.无论是化简还是证明都要注意:
(1)角度的差异与联系;
(2)函数名称间的变换和联系,升降幂,化切为弦是常用手段;
(3)角的范围对三角函数取值、符号的影响;
3.证明及其基本方法: (1)化繁为简法
(2)左右归一法 (3)变更命题法
(4)条件等式的证明关键在于分析已知条件与求证结论之间的区别与联系。
2.三角函数式化简的目标与要求: 化为单角或同角,函数名称少,次数尽量低,尽量不含分母和根号
1.三角函数式的求值的类型一般可分为:
(1)“给角求值”:给出非特殊角求式子的值--化非特殊角为特殊角,再用公式计算;
(2)“给值求值”:给出一些角得三角函数式的值,求另外一些角得三角函数式的值--变换角,找出已知角与所求角的联系;
(3)“给式求值”:给出的三角函数式的值,求其他式子的值--化简已知式或所求式,再求;
(4)“给值求角”:--先求角的某一三角函数值,结合角的范围求出角,要特别注意角的范围对三角函数值的影响,有时需要讨论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com