
12.(2009全国卷Ⅱ理)已知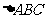 中,
中, , 则
, 则 ( )
( )
A.  B.
B. C.
C. D.
D.

解析:已知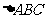 中,
中, ,
, .
.
 故选D.
故选D.
答案 D
11.(2009四川卷文)已知函数 ,下面结论错误的是
,下面结论错误的是
A. 函数 的最小正周期为2
的最小正周期为2
B. 函数 在区间[0,
在区间[0,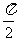 ]上是增函数
]上是增函数
C.函数 的图象关于直线
的图象关于直线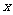 =0对称
=0对称
D. 函数 是奇函数
是奇函数
答案 D
解析∵ ,∴A、B、C均正确,故错误的是D
,∴A、B、C均正确,故错误的是D
[易错提醒]利用诱导公式时,出现符号错误.
10.(2009全国卷Ⅱ文)已知△ABC中, ,则
,则
A.  B.
B.
 C.
C.
 D.
D. 
答案:D
解析:本题考查同角三角函数关系应用能力,先由cotA= 知A为钝角,cosA<0排除A和B,再由
知A为钝角,cosA<0排除A和B,再由 选D
选D
9.(2009北京理)“ ”是“
”是“ ”的
( )
”的
( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案 A
解析 本题主要考查三角函数的基本概念、简易逻辑中充要条件的判断. 属于基础知识、基本运算的考查.
当 时,
时,
反之,当 时,有
时,有 ,
,
或 ,故应选A.
,故应选A.
8.(2009北京文)“ ”是“
”是“ ”的
”的
A. 充分而不必要条件 B.必要而不充分条件
C. 充分必要条件 D.既不充分也不必要条件
答案 A
解析 本题主要考查三角函数的基本概念、简易逻辑中充要条件的判断. 属于基础知识、基本运算的考查.
当 时,
时, ,反之,当
,反之,当 时,
时, ,
,
或 ,故应选A.
,故应选A.
7.(2009全国II文,9)若将函数 的图像向右平移
的图像向右平移 个单位长度后,与函数
个单位长度后,与函数 的图像重合,则
的图像重合,则 的最小值为( )
的最小值为( )
A.  B.
B. C.
C. D.
D.
答案 D
6.(2009全国II文,4) 已知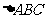 中,
中, , 则
, 则
A.  B.
B. C.
C. D.
D. 
解析:已知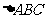 中,
中, ,
, .
.
 故选D.
故选D.
5.(2009全国I文,4)已知tan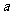 =4,cot
=4,cot =
= ,则tan(a+
,则tan(a+ )= ( )
)= ( )
A. B.
B. C.
C.  D.
D.

答案 B
2. .(2009辽宁理,8)已知函数
.(2009辽宁理,8)已知函数 =Acos(
=Acos( )的图象如图所示,
)的图象如图所示, ,则
,则 =( )
=( )
A. B.
B.  C.-
C.-  D.
D.
答案 C
(2009全国I文,1) °的值为
°的值为
A.  B.
B. C.
C. D.
D. 
答案 A
题型1:象限角


例1.已知角 ;(1)在区间
;(1)在区间 内找出所有与角
内找出所有与角 有相同终边的角
有相同终边的角 ;(2)集合
;(2)集合 ,
, 那么两集合的关系是什么?
那么两集合的关系是什么?


解析:(1)所有与角 有相同终边的角可表示为:
有相同终边的角可表示为: ,
,


则令  ,
,


得 



解得 



从而 或
或



代回 或
或



(2)因为 表示的是终边落在四个象限的平分线上的角的集合;而集合
表示的是终边落在四个象限的平分线上的角的集合;而集合 表示终边落在坐标轴或四个象限平分线上的角的集合,从而:
表示终边落在坐标轴或四个象限平分线上的角的集合,从而: 。
。


点评:(1)从终边相同的角的表示入手分析问题,先表示出所有与角 有相同终边的角,然后列出一个关于
有相同终边的角,然后列出一个关于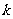 的不等式,找出相应的整数
的不等式,找出相应的整数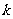 ,代回求出所求解;(2)可对整数
,代回求出所求解;(2)可对整数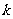 的奇、偶数情况展开讨论。
的奇、偶数情况展开讨论。


例2.若sinθcosθ>0,则θ在( )


A.第一、二象限
B.第一、三象限 


C.第一、四象限 D.第二、四象限


解析:答案:B;∵sinθcosθ>0,∴sinθ、cosθ同号。


当sinθ>0,cosθ>0时,θ在第一象限,当sinθ<0,cosθ<0时,θ在第三象限,因此,选B。


例3.若A、B是锐角△ABC的两个内角,则点P(cosB-sinA,sinB-cosA)在( )


A.第一象限 B.第二象限 C.第三象限 D.第四象限


答案:B


解析:∵A、B是锐角三角形的两个内角,∴A+B>90°,∴B>90°-A,∴cosB<sinA,sinB>cosA,故选B。


例4.已知“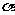 是第三象限角,则
是第三象限角,则 是第几象限角?
是第几象限角?


解法一:因为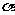 是第三象限角,所以
是第三象限角,所以 ,
,


 ∴
∴ ,
,


∴当k=3m(m∈Z)时, 为第一象限角;
为第一象限角;


当k= 3m+1(m∈Z)时, 为第三象限角,
为第三象限角,


当k= 3m+2(m∈Z)时, 为第四象限角,
为第四象限角,


故 为第一、三、四象限角。
为第一、三、四象限角。


解法二:把各象限均分3等份,再从x轴的正向的上方起.依次将各区域标上I、Ⅱ、Ⅲ、Ⅳ,并依次循环一周,则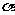 原来是第Ⅲ象限的符号所表示的区域即为
原来是第Ⅲ象限的符号所表示的区域即为 的终边所在的区域。
的终边所在的区域。


由图可知, 是第一、三、四象限角.
是第一、三、四象限角.


点评:已知角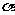 的范围或所在的象限,求
的范围或所在的象限,求 所在的象限是常考题之一,一般解法有直接法和几何法,其中几何法具体操作如下:把各象限均分n等份,再从x轴的正向的上方起,依次将各区域标上I、Ⅱ、Ⅲ、Ⅳ,并循环一周,则
所在的象限是常考题之一,一般解法有直接法和几何法,其中几何法具体操作如下:把各象限均分n等份,再从x轴的正向的上方起,依次将各区域标上I、Ⅱ、Ⅲ、Ⅳ,并循环一周,则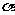 原来是第几象限的符号所表示的区域即为
原来是第几象限的符号所表示的区域即为 (n∈N*)的终边所在的区域。
(n∈N*)的终边所在的区域。


题型2:三角函数定义


例5.已知角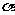 的终边过点
的终边过点 ,求
,求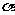 的四个三角函数值。
的四个三角函数值。


解析:因为过点 ,所以
,所以 ,
, 。
。


当 ;
;


 ,
, 。
。


当 ,
, ;
; 。
。


例6.已知角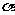 的终边上一点
的终边上一点 ,且
,且 ,求
,求 的值。
的值。
解析:由题设知 ,
, ,所以
,所以 ,
,
得 ,
,
从而
 ,
,
解得 或
或 。
。
当 时,
时, ,
,  ;
;
当 时,
时, ,
,  ;
;
当 时,
时, ,
,  。
。
题型3:诱导公式
例7.(2009辽宁文,8)已知 ,则
,则 ( )
( )
A. B.
B. C.
C. D.
D.
答案 D
例8.化简:
(1) ;
;
(2) 。
。
解析:(1)原式 ;
;
(2)①当 时,原式
时,原式 。
。
②当 时,原式
时,原式 。
。
点评:关键抓住题中的整数 是表示
是表示 的整数倍与公式一中的整数
的整数倍与公式一中的整数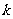 有区别,所以必须把
有区别,所以必须把 分成奇数和偶数两种类型,分别加以讨论.
分成奇数和偶数两种类型,分别加以讨论.
题型4:同角三角函数的基本关系式
例9.已知 ,试确定使等式成立的角
,试确定使等式成立的角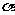 的集合。
的集合。
解析:∵
 ,
,
= =
= =
= 。
。
又∵ ,
,
∴
 ,
,
即得 或
或 .
.
所以,角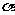 的集合为:
的集合为: 或
或 。
。
例10.(1)证明: ;
;
(2)求证: 。
。
解析:(1)分析:证明此恒等式可采取常用方法,也可以运用分析法,即要证 ,只要证A·D=B·C,从而将分式化为整式.
,只要证A·D=B·C,从而将分式化为整式.
证法一:右边=
=

=
证法二:要证等式,即为

只要证
2( )(
)( )=
)=
即证:

 ,
,
即1= ,显然成立,
,显然成立,
故原式得证。
点评:在进行三角函数的化简和三角恒等式的证明时,需要仔细观察题目的特征,灵活、恰当地选择公式,利用倒数关系比常规的“化切为弦”要简洁得多。(2)同角三角函数的基本关系式有三种,即平方关系、商的关系、倒数关系.
(2)证法一:由题义知 ,所以
,所以 。
。
∴左边=
 右边。
右边。
∴原式成立。
证法二:由题义知 ,所以
,所以 。
。
又∵ ,
,
∴ 。
。
证法三:由题义知 ,所以
,所以 。
。


 ,
,
∴ 。
。
点评:证明恒等式的过程就是分析、转化、消去等式两边差异来促成统一的过程,证明时常用的方法有:(1)从一边开始,证明它等于另一边(如例5的证法一);(2)证明左右两边同等于同一个式子(如例6);(3)证明与原式等价的另一个式子成立,从而推出原式成立
(以下来自2009年各地高考试题)
1.(2009海南宁夏理,5).有四个关于三角函数的命题:
 :
: x
x R,
R, 
 +
+
 =
=
 :
:  x、y
x、y R,
sin(x-y)=sinx-siny
R,
sin(x-y)=sinx-siny
 :
:  x
x
 ,
, =sinx
=sinx  :
sinx=cosy
:
sinx=cosy x+y=
x+y=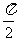
其中假命题的是
A. ,
, B.
B. ,
, C.
C. ,
, D.
D. ,
,
答案 A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com