
9. 若数列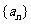 为等差(比)数列,则
为等差(比)数列,则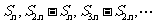 也是等差(比)数列;
也是等差(比)数列;
8.若{an}、{bn}是等差数列,则{kan+pbn}(k、p是非零常数)是等差数列;若{an}、{bn}是等比数列,则{kan}、{anbn}等也是等比数列;
7. 当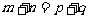 时,对等差数列有
时,对等差数列有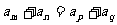 ;对等比数列有
;对等比数列有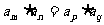 ;
;
6. 在等差数列中,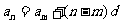 ,
,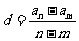 ;在等比数列中,
;在等比数列中,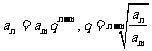 ;
;
5.熟记等差、等比数列的定义,通项公式,前n项和公式,在用等比数列前n项和公式时,勿忘分类讨论思想;
4.首项为正(或为负)的递减(或递增)的等差数列前n项和的最大(或最小)问题,转化为解不等式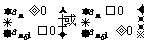 解决;
解决;
3.等比数列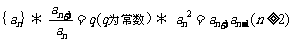
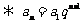 ;
;
2.等差数列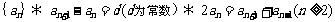
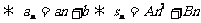 ;
;
1.由Sn求an,an={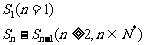 注意验证a1是否包含在后面an 的公式中,若不符合要单独列出。一般已知条件中含an与Sn的关系的数列题均可考虑用上述公式;
注意验证a1是否包含在后面an 的公式中,若不符合要单独列出。一般已知条件中含an与Sn的关系的数列题均可考虑用上述公式;
15.实系数一元二次方程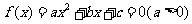 的两根
的两根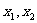 的分布问题:
的分布问题:
|
根的情况 |
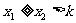 |
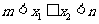 |
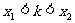 |
|
等价命题 |
在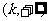 上有两根 上有两根 |
在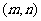 上有两根 上有两根 |
在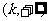 和 和 上各有一根 上各有一根 |
|
充要条件 |
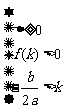 |
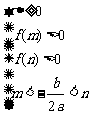 |
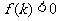 |
注意:若在闭区间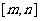 讨论方程
讨论方程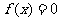 有实数解的情况,可先利用在开区间
有实数解的情况,可先利用在开区间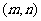 上实根分布的情况,得出结果,在令
上实根分布的情况,得出结果,在令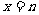 和
和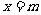 检查端点的情况。
检查端点的情况。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com