
4.原点和点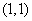 在直线
在直线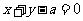 的两侧,则
的两侧,则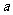 的取值范围是
.
的取值范围是
.
3. 给出平面区域(包括边界)如图所示,若使目标函数
给出平面区域(包括边界)如图所示,若使目标函数
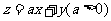 取得最大值的最优解有无穷多个,
取得最大值的最优解有无穷多个,
则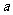 的值为( )
的值为( )
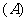
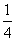
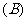
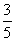
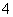
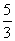
2.表示图中阴影部分的二元一次不等式组是 ( )
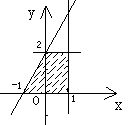
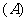

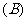


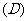

1.不等式 表示的平面区域在直线
表示的平面区域在直线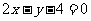 的 (
)
的 (
)
 左上方
左上方
 右上方
右上方  左下方
左下方  右下方
右下方
2、了解线性规划的意义,并会进行简单的应用
(1) 能结合实例说明线性约束条件、线性目标函数、可行解、可行域、最优解等基本概念;
(2) 能叙述线性规划问题的意义;
(3) 知道线性规划问题图解法的基本步骤,并能运用它解决一些简单的实际问题;
(4) 学会把实际问题转化为线性规划问题的一般方法;
1、了解二元一次不等式表示平面区域
(1) 能用语言表述二元一次不等式及不等式组,能用数学符号表示二元一次不等式及不等式组;
(2) 知道以二元一次不等式的所有解为坐标的点在平面内所表示的平面区域的特性;
(3) 能画出一个二元一次不等式及不等式组所表示的平面区域;
2、线性规划
⑴ 基本概念
|
名 称 |
意
义 |
|
线性约束条件 |
由x,y的一次不等式(或方程)组成的不等式组,是对x,y的约束条件 |
|
目标函数 |
关于x,y的解析式 |
|
线性目标函数 |
关于x,y的一次解析式 |
|
可行解 |
满足线性约束条件的解(x,y)叫做可行解 |
|
可行域 |
所有可行解组成的集合叫做可行域 |
|
最优解 |
使目标函数达到最大值或最小值的可行解 |
|
线性规划问题 |
求线性目标函数在线性约束条件下的最大值或最小值的问题 |
⑵用图解法解决线性规划问题的一般步骤
①、设出所求的未知数
②、列出约束条件(即不等式组)
③、建立目标函数
④、作出可行域
⑤、运用图解法求出最优解
1、二元一次不等式表示平面区域
(1)一般地,二元一次不等式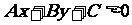 在平面直角坐标系中表示直线
在平面直角坐标系中表示直线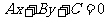 某一侧的所有点组成的平面区域(半平面)不含边界线.
某一侧的所有点组成的平面区域(半平面)不含边界线.
不等式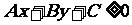 所表示的平面区域(半平面)包括边界线.
所表示的平面区域(半平面)包括边界线.
(2)对于直线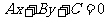 同一侧的所有点(x,y),使得
同一侧的所有点(x,y),使得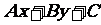 的值符号相同。因此,如果直线
的值符号相同。因此,如果直线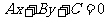 一侧的点使
一侧的点使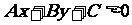 ,另一侧的点就使
,另一侧的点就使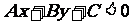 。所以判定不等式
。所以判定不等式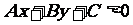 (或
(或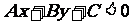 )所表示的平面区域时,只要在直线
)所表示的平面区域时,只要在直线 的一侧任意取一点
的一侧任意取一点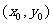 ,将它的的坐标代入不等式,如果该点的坐标满足不等式,不等式就表示该点所在一侧的平面区域;如果不满足不等式,就表示这个点所在区域的另一侧平面区域。
,将它的的坐标代入不等式,如果该点的坐标满足不等式,不等式就表示该点所在一侧的平面区域;如果不满足不等式,就表示这个点所在区域的另一侧平面区域。
(3) 由几个不等式组成的不等式组表示的平面区域是各个不等式所表示的平面区域的公共部分.
12.已知正方形的中心为直线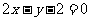 和
和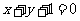 的交点,正方形一边所在直线的方程为
的交点,正方形一边所在直线的方程为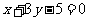 ,求其它三边所在的直线方程.
,求其它三边所在的直线方程.
11.已知三条直线 :
: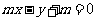 ,
, :
: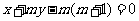 ,
,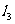 :
: ,它们围成
,它们围成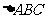 .
.
(1)求证:不论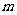 取何值时,
取何值时,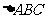 中总有一个顶点为定点;
中总有一个顶点为定点;
(2)当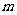 取何值时,
取何值时,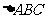 的面积取最大值、最小值?并求出最大值、最小值.
的面积取最大值、最小值?并求出最大值、最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com