
2.求函数y= (
(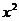 -4x)的单调递增区间
-4x)的单调递增区间
解:先求定义域:由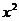 -4x>0得x(x-4)>0
-4x>0得x(x-4)>0
∴x<0或x>4
又函数y= t是增函数
t是增函数
故所求单调递增区间为t=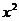 -4x在定义域内的单调递增区间
-4x在定义域内的单调递增区间
∵t=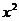 -4x的对称轴为x=2
-4x的对称轴为x=2
∴所求单调递增区间为:(4,+∞)
1.求y=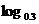 (
(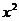 -2x)的单调递减区间
-2x)的单调递减区间
解:先求定义域:由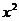 -2x>0,得x(x-2)>0
-2x>0,得x(x-2)>0
∴x<0或x>2
∵函数y=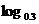 t是减函数
t是减函数
故所求单调减区间即t=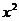 -2x在定义域内的增区间
-2x在定义域内的增区间
又t=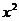 -2x的对称轴为x=1
-2x的对称轴为x=1
∴所求单调递减区间为(2,+∞)
例1 ⑴证明函数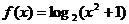 在
在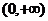 上是增函数
上是增函数
⑵函数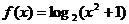 在
在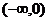 上是减函数还是增函数?
上是减函数还是增函数?
⑴证明:设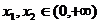 ,且
,且
则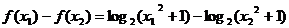
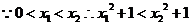

又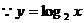 在
在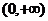 上是增函数
上是增函数
∴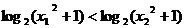 即
即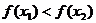
∴函数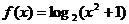 在
在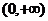 上是增函数
上是增函数
⑵解:是减函数,证明如下:
设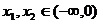 ,且
,且
则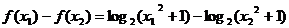
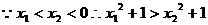
又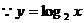 在
在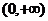 上是增函数
上是增函数
∴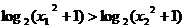 即
即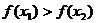
∴函数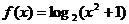 在
在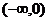 上是减函数
上是减函数
小结:复合函数的单调性
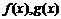 的单调相同,
的单调相同,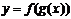 为增函数,否则为减函数
为增函数,否则为减函数
例2 求函数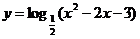 的单调区间,并用单调定义给予证明
的单调区间,并用单调定义给予证明
解:定义域 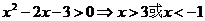
单调减区间是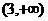 设
设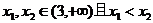 则
则
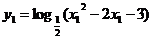
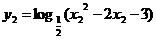
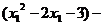
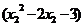 =
=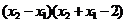
∵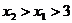 ∴
∴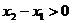
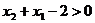
∴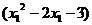 >
>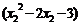 又底数
又底数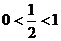
∴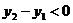 即
即 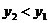
∴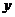 在
在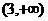 上是减函数
上是减函数
同理可证: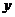 在
在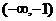 上是增函数
上是增函数
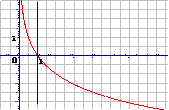
2.对数函数的性质:
|
|
a>1 |
0<a<1 |
|
图 象 |
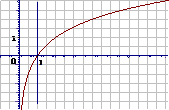 |
 |
|
性 质 |
定义域:(0,+∞) |
|
|
值域:R |
||
过点(1,0),即当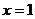 时, 时,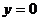 |
||
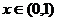 时 时 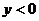  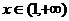 时 时 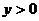  |
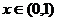 时 时 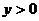  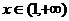 时 时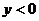  |
|
在(0,+∞)上是增函数 |
在(0,+∞)上是减函数 |
1.判断及证明函数单调性的基本步骤:假设-作差-变形-判断
22.(本小题满分14分)
设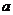 为实数,函数
为实数,函数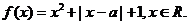
(Ⅰ)讨论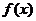 的奇偶性;
的奇偶性;
(Ⅱ)求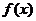 在
在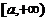 上的最小值.
上的最小值.
(Ⅲ)求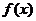 在
在 上的最小值.
上的最小值.
21.(本小题满分12分)
某市居民自来水收费标准如下:每户每月用水不超过4吨时每吨为1.80元,当用水超过4吨时,超过部分每吨3.00元,某月甲、乙两户共交水费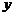 元,已知甲、乙两用户 该月用水量分别为
元,已知甲、乙两用户 该月用水量分别为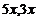 (吨)。
(吨)。
(1)求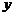 关于
关于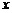 的函数;
的函数;
(2)若甲、乙两户该月共交水费26.4元,分别求出甲、乙两户该月的用水量和水费。(精确到0.1)
20.(本小题满分12分)
已知定义域为R的函数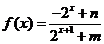 是奇函数。
是奇函数。
①求m、n的值。
②若对任意的t∈R,不等式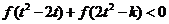 恒成立,求实数k的取值范围。
恒成立,求实数k的取值范围。
19.(本题满分12分)
定义在R上的函数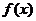 满足
满足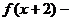
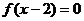 ,
,
当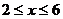 时,
时,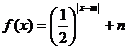 且
且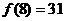
(1)求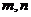 的值.
(2)比较
的值.
(2)比较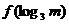 与
与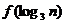 的大小
的大小
18. (本小题满分12分)
给定两个命题:
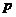 :对任意实数
:对任意实数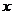 都有
都有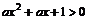 恒成立;
恒成立;
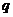 :关于
:关于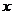 的方程
的方程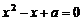 有实数根;
有实数根;
如果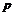 与
与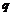 中有且仅有一个为真命题,求实数
中有且仅有一个为真命题,求实数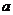 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com