7．(2009·保定市调研)在数列1,3,2，…中，前两项以后的每一项等于它前面两项之差(前面一项减去再前面一项)，则该数列的前100项之和是(　)

A．5　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．20

C．300　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．652

答案：A

解析：∵在数列1,3,2，…中，a_n＝a_n－1－a_n－2(n≥3)，∴a₄＝－1，a₅＝－3，a₆＝－2，a₇＝1，a₈＝3，…，即数列{a_n}是一个周期为6的周期数列，故其前100项的和为：

S₁₀₀＝16×[1+3+2+(－1)+(－3)+(－2)]+1+3+2+(－1)＝5，故选A.

6．若数列{a_n}的通项公式a_n＝，记f(n)＝2(1－a₁)(1－a₂)…(1－a_n)，试通过计算f(1)，f(2)，f(3)的值，推测出f(n)为(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

答案：C

解析：f(1)＝2(1－a₁)＝＝，

f(2)＝2(1－)(1－)＝＝，

f(3)＝2(1－a₁)(1－a₂)(1－a₃)

＝2(1－)(1－)(1－)＝＝，

可猜测f(n)＝.

5．(2009·咸阳模拟)已知数列{a_n}的前n项和S_n＝n²－9n，第k项满足5<a_k<8，则k等于(　)

A．9　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．8

C．7　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．6

答案：B

解析：∵S_n＝n²－9n，

∴当n≥2时，a_n＝S_n－S_n－1＝2n－10.

又当n＝1时，a₁＝S₁＝－8也适合上式，

∴a_n＝2n－10，又5<2k－10<8，<k<9，

∴k＝8.

4．下图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案，则按此规律第n个图案中需用黑色瓷砖________块．(用含n的代数式表示)

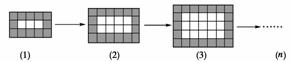
A．4n　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．4n+1

C．4n－3　 　　　　　　　　　　　　　　　　　　　　　　　　　 D．4n+8

答案：D

解析：第(1)、(2)、(3)…个图案黑色瓷砖数依次为：15－3＝12；24－8＝16；35－15＝20；….由此可猜测第(n)个图案黑色瓷砖数为：12+(n－1)×4＝4n+8.

3．数列－1，，－，，…的一个通项公式a_n是(　)

A．(－1)ⁿ　 　　　　　　　　　　　　　　　　　　　　 B．(－1)ⁿ

C．(－1)ⁿ　 　　　　　　　　　　　　　　　　　 D．(－1)ⁿ

答案：D

解析：将数列中的各项变为－，，

－，，…，故其通项a_n＝(－1)ⁿ.

2．数列{a_n}中，a₁＝1，对于所有的n≥2，n∈N^*都有a₁·a₂·a₃·…·a_n＝n²，则a₃+a₅等于(　)

A.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D.

答案：A

解法一：由已知得a₁·a₂＝2²，∴a₂＝4.

a₁·a₂·a₃＝3²，∴a₃＝，

a₁·a₂·a₃·a₄＝4²，∴a₄＝，

a₁·a₂·a₃·a₄·a₅＝5²，∴a₅＝.

∴a₃+a₅＝+＝.

解法二：由a₁·a₂·a₃·…·a_n＝n²，得a₁·a₂·a₃·…·a_n－1＝(n－1)²，∴a_n＝()²(n≥2)，

∴a₃+a₅＝()²+()²＝.

1．数列1,2,2,3,3,3,4,4,4,4,5，…的第100项是(　)

A．14　　　　　　　　　　　　　　　　　 B．12

C．13　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．15

答案：A

解析：易知数字为n时共有n个，到数字n时，总共的数字的个数为1+2+3+…+n＝.易知n＝13时，最后一项为91，n＝14共有14个，故第100项为14.

15．有6个房间安排4个人居住，每人可以进住任一房间，且进住房间是等可能的，试求下列各事件的概率：

(1)事件A：指定的4个房间中各有一人；

(2)事件B：恰有4个房间各有一人；

(3)事件C：指定的某个房间中有两人；

(4)事件D：第一号房间有一人，第二号房间有三人．

解：由于每个人可以进住任一房间，则4个人进住6个房间共有6⁴种方法．

(1)指定的4个房间中各有一人，有A种方法，

∴P(A)＝＝.

(2)恰有4个房间各有一人的进住方法有C·A种，

∴P(B)＝＝.

(3)从4个人中选出2人去指定的某个房间，有C种方法，其余2人各有5种进住方法，总共有C×5×5种进住方法，

∴P(C)＝＝.

(4)选一人进住一号房间，有C种方法，余下三人进住第二号房间，只有一种方法，共有C＝4种方法，

∴P(D)＝＝.

14．(2009·海南，宁夏文)为了了解《中华人民共和国道路交通安全法》在学生中的普及情况，调查部门对某校6名学生进行问卷调查，6人得分情况如下：

5,6,7,8,9,10.

把这6名学生的得分看成一个总体．

(1)求该总体的平均数；

(2)用简单随机抽样方法从这6名学生中抽取2名，他们的得分组成一个样本．求该样本平均数与总体平均数之差的绝对值不超过0.5的概率．

解：(1)总体平均数为(5+6+7+8+9+10)＝7.5.

(2)设A表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”．

从总体中抽取2个个体全部可能的基本结果有：

(5,6)，(5,7)，(5,8)，(5,9)，(5,10)，(6,7)，(6,8)，(6,9)，(6,10)，(7,8)，(7,9)，(7,10)，(8,9)，(8,10)，(9,10)，共15个基本结果．

事件A包括的基本结果有：(5,9)，(5,10)，(6,8)，(6,9)，(6,10)，(7,8)，(7,9)，共有7个基本结果．

所以所求的概率为P(A)＝.

13．箱中有a个正品，b个次品，从箱中随机连续抽取3次，在以下两种抽样方式下：(1)每次抽样后不放回；(2)每次抽样后放回．求取出的3个全是正品的概率．

解：(1)若不放回抽样3次看作有顺序，则从a+b个产品中不放回抽样3次共有A种方法，从a个正品中不放回抽样3次共有A种方法，可以抽出3个正品的概率P＝.若不放回抽样3次看作无顺序，则从a+b个产品中不放回抽样3次共有C种方法，从a个正品中不放回抽样3次共有C种方法，可以取出3个正品的概率P＝.两种方法结果一致．

(2)从a+b个产品中有放回的抽取3次，每次都有a+b种方法，所以共有(a+b)³种不同的方法，而3个全是正品的抽法共有a³种，所以3个全是正品的概率

P＝＝³.