
21.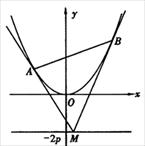 (12分)如图,设抛物线方程为
(12分)如图,设抛物线方程为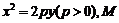 直线
直线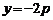 上任意一点,过M引抛物线的切线,切点分别为A,B。
上任意一点,过M引抛物线的切线,切点分别为A,B。
(1)求证:A,M,B三点的横坐标成等差数列;
(2)已知当M点的坐标为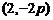 时,
时,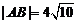 ,求此时抛物线的方程;
,求此时抛物线的方程;
20.(12分)已知函数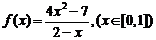 。(1)求函数
。(1)求函数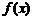 的单调区间和值域;
的单调区间和值域;
(2)设 ,函数
,函数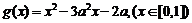 ,若对于任意
,若对于任意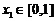 总存在
总存在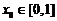 ,使得
,使得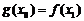 成立,求实数
成立,求实数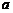 的取值范围。
的取值范围。
19.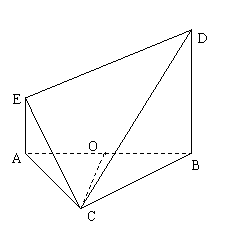 (12分)如图,等边
(12分)如图,等边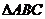 与直角梯形ABDE所在平面垂直,
与直角梯形ABDE所在平面垂直,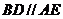 ,AE⊥AB,
,AE⊥AB,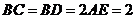 ,O为AB的中点.
,O为AB的中点.
(1)证明: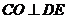 ;
;
(2)求二面角 的余弦值.
的余弦值.
2. 如果引爆或子弹打光停止射击,请通过计算证明:停止射击的概率必然为1。
1. 求油罐被引爆的概率;
18.(12分)在一次抗洪抢险中准备用射击的方法引爆从上游漂流而下的一个巨大汽油罐。已知只有5发子弹,第一次命中只能使汽油流出,第二次命中才能引爆。每次射击是相互独立的,且命中的概率都是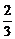 。
。
17.(12分)已知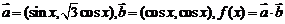 。(1)若
。(1)若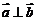 ,求
,求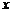 的取值集合;
的取值集合;
(2)求函数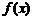 的周期及增区间。
的周期及增区间。
15.________________________________; 16.___________________________________。
13.________________________________; 14.___________________________________;
16.有以下命题:①若集合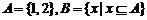 ,则
,则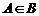 ;②二项式
;②二项式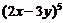 的展开式的各项的系数和为
的展开式的各项的系数和为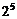 ;③已知函数
;③已知函数 在
在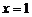 处取得极值,则实数
处取得极值,则实数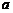 的值是
的值是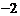 或
或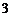 ;④已知点
;④已知点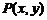 是抛物线
是抛物线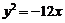 的准线与双曲线
的准线与双曲线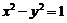 的两条渐近线所围成的三角形区域(含边界)内的任意一点,则
的两条渐近线所围成的三角形区域(含边界)内的任意一点,则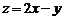 的最大值为9。其中正确命题的序号有__________
的最大值为9。其中正确命题的序号有__________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com