
16.(浙江18)在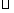 ABC中,角A、B、C所对应的边分别为a、b、c,且满足
ABC中,角A、B、C所对应的边分别为a、b、c,且满足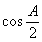 =
=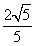 ,
,
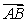
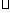
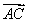 =3.
=3.
(Ⅰ)求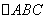 的面积;
的面积; 

(Ⅱ)若b+c=6,求a的值。
解析:(I)因为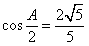 ,
,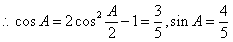 ,又由
,又由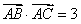 ,得
,得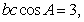
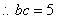 ,
,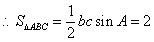
(II)对于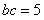 ,又
,又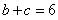 ,
,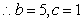 或
或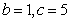 ,由余弦定理得
,由余弦定理得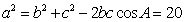 ,
,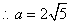
15.(浙江8)已知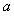 是实数,则函数
是实数,则函数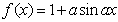 的图象不可能是
的图象不可能是 ( )
( )
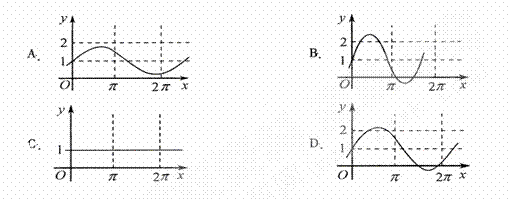
D
[解析]对于振幅大于1时,三角函数的周期为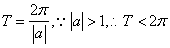 ,而D不符合要求,它的振幅大于1,但周期反而大于了
,而D不符合要求,它的振幅大于1,但周期反而大于了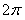 .
.
14.(江苏15)设向量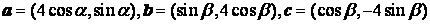 (1)若
(1)若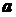 与
与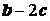 垂直,求
垂直,求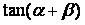 的值;
的值;
(2)求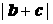 的最大值;
的最大值;
(3)若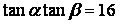 ,求证:
,求证: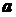 ∥
∥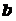 .
.
[解析] 本小题主要考查向量的基本概念,同时考查同角三角函数的基本关系式、二倍角的正弦、两角和的正弦与余弦公式,考查运算和证明得基本能力。满分14分。

13.(江苏4)函数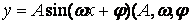 为常数,
为常数,
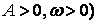 在闭区间
在闭区间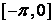 上的图象如图所示,则
上的图象如图所示,则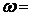 .
.
[解析] 考查三角函数的周期知识。
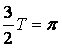 ,
,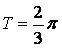 ,所以
,所以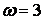 ,
,
12.(广东16)已知向量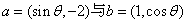 互相垂直,其中
互相垂直,其中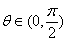 .
.
(1)求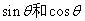 的值;
的值;
(2)若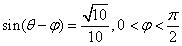 ,求
,求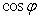 的值.
的值.
解:(1)∵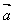 与
与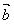 互相垂直,则
互相垂直,则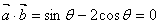 ,即
,即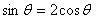 ,代入
,代入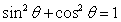 得
得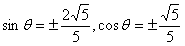 ,又
,又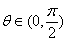 ,∴
,∴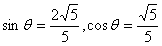 .
.
 (2)∵
(2)∵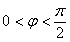 ,
,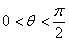 ,∴
,∴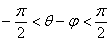 ,则
,则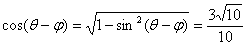 ,∴
,∴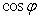
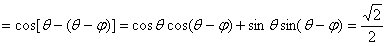 .
.
11.(福建
1)函数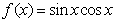 最小值是
最小值是
A.-1
B. 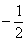 C.
C.
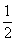 D.1
D.1
10.(湖北17)已知向量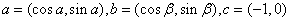
(Ⅰ)求向量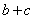 的长度的最大值;
的长度的最大值;
(Ⅱ)设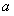
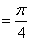 ,且
,且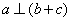 ,求
,求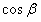 的值。
的值。
解析:(1)解法1: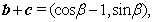 则
则
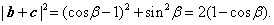
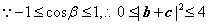 ,即
,即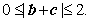


当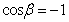 时,有
时,有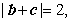 所以向量
所以向量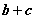 的长度的最大值为2.
的长度的最大值为2.
解法2: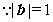 ,
,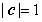 ,
,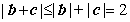
当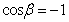 时,有
时,有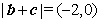 ,即
,即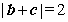 ,
,
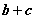 的长度的最大值为2.
的长度的最大值为2.
(2)解法1:由已知可得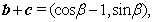
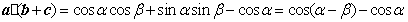 。
。
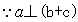 ,
,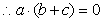 ,即
,即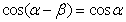 。
。
由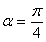 ,得
,得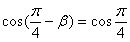 ,即
,即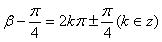 。
。
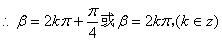 ,于是
,于是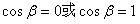 。
。 

解法2:若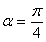 ,则
,则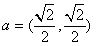 ,又由
,又由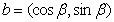 ,
,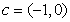 得
得
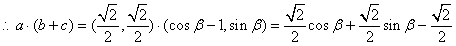
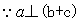 ,
,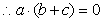 ,即
,即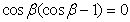
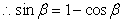 ,平方后化简得
,平方后化简得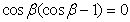


解得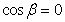 或
或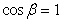 ,经检验,
,经检验,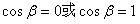 即为所求
即为所求
9.(北京15)在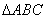 中,角
中,角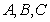 的对边分别为
的对边分别为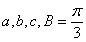 ,
,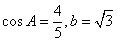 。
。
(I)求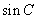 的值;
的值;
(Ⅱ)求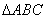 的面积。
的面积。
[解析]本题主要考查三角形中的三角函数变换及求值、诱导公式、三角形的面积公式等基础知识,主要考查基本运算能力.
(Ⅰ)∵A、B、C为△ABC的内角,且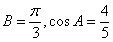 ,
,
∴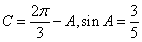 ,
,
∴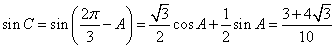 .
.
(Ⅱ)由(Ⅰ)知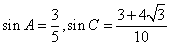 ,
, 

又∵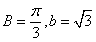 ,∴在△ABC中,由正弦定理,得
,∴在△ABC中,由正弦定理,得
∴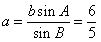 .
.
∴△ABC的面积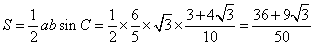
8.(山东17)设函数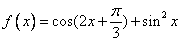 。
。
(Ⅰ)求函数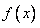 的最大值和最小正周期;
的最大值和最小正周期; 

(Ⅱ)设A,B,C为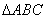 的三个内角,若
的三个内角,若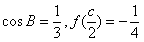 ,且C为锐角,求
,且C为锐角,求
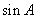 。
。
解:
(1)f(x)=cos(2x+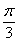 )+sin
)+sin x.=
x.=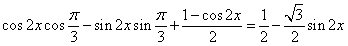
所以函数f(x)的最大值为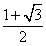 ,最小正周期
,最小正周期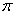 .
. 

(2)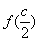 =
=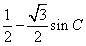 =-
=-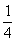 , 所以
, 所以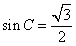 , 因为C为锐角, 所以
, 因为C为锐角, 所以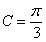 ,
,
又因为在 ABC 中, cosB=
ABC 中, cosB=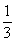 , 所以
, 所以 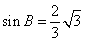 , 所以
, 所以 

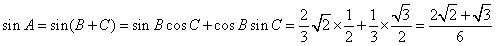 .
.
[命题立意]:本题主要考查三角函数中两角和差的弦函数公式、二倍角公式、三角函数的性质以及三角形中的三角关系.
7.(山东3)将函数y=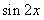 的图像向左平移
的图像向左平移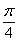 个单位,再向上平移1个单位,所得图像的函数解析式是
个单位,再向上平移1个单位,所得图像的函数解析式是
(A)y=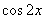 (B)y=
(B)y=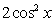
(C)y=1+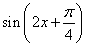 (D)y=
(D)y=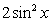
[解析]:将函数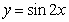 的图象向左平移
的图象向左平移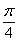 个单位,得到函数
个单位,得到函数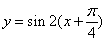 即
即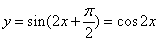 的图象,再向上平移1个单位,所得图象的函数解析式为
的图象,再向上平移1个单位,所得图象的函数解析式为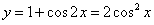 ,故选B.
,故选B.
答案:B
[命题立意]:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com