
19.对数的换底公式及它的变形,你掌握了吗?(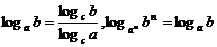 )
)
18.解对数函数问题时,你注意到真数与底数的限制条件了吗?(真数大于零,底数大于零且不等于1)字母底数还需讨论呀.
例:函数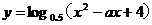 的值域是R,则
的值域是R,则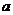 的取值范围是 。(
的取值范围是 。(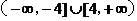 )
)
17.抽象函数的单调性、奇偶性一定要紧扣函数性质利用单调性、奇偶性的定义求解。同时,要领会借助函数单调性利用不等关系证明等式的重要方法:f(a)≥b且f(a)≤bÛf(a)=b。
16.切记定义在R上的奇函数y=f(x)必定过原点。
15.你知道函数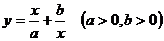 的单调区间吗?(该函数在
的单调区间吗?(该函数在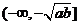 或
或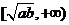 上单调递增;在
上单调递增;在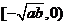 或
或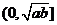 上单调递减,求导易证)这可是一个应用广泛的函数!请你着重复习它的特例“对号函数”
上单调递减,求导易证)这可是一个应用广泛的函数!请你着重复习它的特例“对号函数”
14.根据定义证明函数的单调性时,规范格式是什么?(取值, 作差, 判正负.)用导数研究函数单调性时,一定要注意“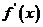 >0(或
>0(或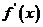 <0)是该函数在给定区间上单调递增(减)的必要条件。
<0)是该函数在给定区间上单调递增(减)的必要条件。
13.原函数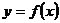 在区间
在区间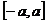 上单调递增,则一定存在反函数,且反函数
上单调递增,则一定存在反函数,且反函数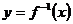 也单调递增;但一个函数存在反函数,此函数不一定单调.判断一个函数的奇偶性时,你注意到函数的定义域是否关于原点对称这个必要非充分条件了吗?特例:
也单调递增;但一个函数存在反函数,此函数不一定单调.判断一个函数的奇偶性时,你注意到函数的定义域是否关于原点对称这个必要非充分条件了吗?特例: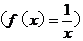
12.函数与其反函数之间的一个有用的结论: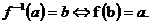 原函数与反函数图象的交点不全在y=x上(例如:
原函数与反函数图象的交点不全在y=x上(例如: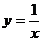 );
);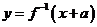 只能理解为
只能理解为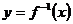 在x+a处的函数值。
在x+a处的函数值。
11.求二次函数的最值问题时你注意到x的取值范围了吗?
例:已知(x+2)2+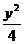 =1,求x2+y2的取值范围。(由于(x+2)2+
=1,求x2+y2的取值范围。(由于(x+2)2+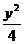 =1得(x+2)2=1-
=1得(x+2)2=1-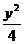 ≤1,∴-3≤x≤-1从而当x=-1时x2+y2有最小值1。x2+y2的取值范围是[1,
≤1,∴-3≤x≤-1从而当x=-1时x2+y2有最小值1。x2+y2的取值范围是[1, 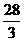 ])
])
10.求一个函数的解析式和一个函数的反函数时,你注明了该函数的定义域了吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com