24．(1)当a=0时，0<0不成立，原不等式的解集为Ф；

当a<0时，不等式的解集也为Ф；当a>0时，不等式即|x|<1，∴解集为{x|-1<x<1}．

(2)原不等式即(a-1)x≤b+2，

1⁰当a>1时，a-1>0，∴此时不等式的解集为{x|x≤}，

2⁰当a<1时，a-1<0，∴此时不等式的解集为{x|x≥}，

3⁰当a=1时，a-1=0，若b≥-2，则不等式的解集为实数集R，

　　　　　　　　　 若b<-2，则不等式的解集为Ф．

24．解下列关于x的不等式：

(1)|ax|<a；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (2)ax-2≤x+b．

23．解下列不等式：

(1)|5x-4|≥6；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (2)3-|-2x-1|>0；　　　　　 (3)1≤||<3．

[解答](1)即5x-4≤-6，或5x-4≥6，解得，或；

(2)即|2x+1|<3，∴-3<2x+1<3，解得-2<x<1；

(3)原不等式等价于不等式组

即

∴原不等式的解集为{x|-12<x≤-8，或-4≤x<0}．

22．已知对于任意的实数x，不等式|x+1|-|x-2|>k恒成立，求出实数k的取值范围．

[解答一]∵

∴，欲不等式|x+1|-|x-2|>k恒成立，当且仅当k小于的最小值时，∴k的取值范围是()．

[解答二]要使不等式|x+1|-|x-2|>k恒成立，只要代数式|x+1|-|x-2|的最小值大于k，反之即要求k小于代数式|x+1|-|x-2|的最小值；

注意到|x+1|的几何意义为数轴上的点x到-1的距离，|x-2|的几何意义为点x到2的距离，由于这两个距离之差的最小值显然是-3，∴只需k<-3．故k的取值范围是()．

21．解不等式|2-|2x+1||>1．

[解答]原不等式等价于2-|2x+1|<-1，或2-|2x+1|>1，

即|2x+1|>3，或|2x+1|<1，

由|2x+1|>3，得2x+1<-3，或2x+1>3，∴x<-2，或x>1；

由|2x+1|<1，得-1<2x+1<1，∴-1<x<0；

综合以上得原不等式的解集是{x|x<-2，或-1<x<0，或x>1}．

20．解不等式|．

[解答]若，则原不等式化为不等式组

解这一不等式组得；

若，则原不等式化为不等式组

此时解得；

综上得原不等式的解集是}．

19．已知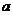为实数，且关于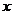的不等式的解集是，则关于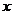

的不等式的解集是___________．

[答案]R

提示：若a≤1则不等式的解集是空集，故在已知条件下有，

∴不等式的右边是一个负数，由绝对值的意义知这一不等式对于任意实数x都成立，∴所求解集为实数集R．

18．不等式2≤|3x-4|<3的解集是______________．

[答案]

提示：令3x-4=y，则不等式等价于不等式组即

∴，即，

解这一对应的一元一次不等式组，得原不等式的解集是．

17．已知实数a≠0，则关于x的不等式|ax+3|<2的解集是_____________．

[答案]时为；时为

提示：原不等式即，∴，若，则原不等式解集为；若，则原不等式的解集为．

16．设全集为R，已知集合M={x||4x|≥13}，集合P={x||x|≤2a，a>0}，若M∩P是非空集合，且集合M∩P所对应的区间长度之和为，则a=___________．

[答案]2

提示：由已知得M={或}，P=，利用数轴表示出集合M∩P，可得M∩P={x|-2a≤x≤-，或≤x≤2a}，由此知M∩P所对应的区间长度之和为2(2a-)=，解得a=2．