
15.排成一排的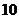 名学生生日的月份均不相同,有
名学生生日的月份均不相同,有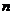 名教师,依次挑选这些学生参加
名教师,依次挑选这些学生参加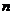 个兴趣小组,每个学生恰被一名教师挑选,且保持学生的排序不变,每名教师挑出的学生必须满足生日的月份是逐渐增加或逐渐减少的(挑选一名或两名学生也认为是逐渐增加或逐渐减少的),每名教师尽可能多选学生,对于学生所有可能的排序,求
个兴趣小组,每个学生恰被一名教师挑选,且保持学生的排序不变,每名教师挑出的学生必须满足生日的月份是逐渐增加或逐渐减少的(挑选一名或两名学生也认为是逐渐增加或逐渐减少的),每名教师尽可能多选学生,对于学生所有可能的排序,求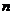 的最小值。
的最小值。
解 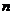 的最小值为
的最小值为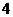 。
。
若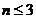 ,不妨假设这
,不妨假设这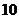 名学生生日的月份分别为
名学生生日的月份分别为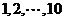 ,当学生按生日排序为
,当学生按生日排序为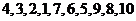 时,存在一名教师至少要挑选前四名学生中的两名,由于这两名学生生日的月份是逐渐减少的,且后六名学生生日的月份均大于前四名学生生日的月份,因此这名教师不可能再挑选后六名学生;在余下的不超过两名教师中,一定存在一名教师至少要挑选第五名至第七名学生中的两名,同理,这名教师不可能再挑选后三名学生;余下的不超过一名教师也不可能挑选后三名学生,矛盾。
时,存在一名教师至少要挑选前四名学生中的两名,由于这两名学生生日的月份是逐渐减少的,且后六名学生生日的月份均大于前四名学生生日的月份,因此这名教师不可能再挑选后六名学生;在余下的不超过两名教师中,一定存在一名教师至少要挑选第五名至第七名学生中的两名,同理,这名教师不可能再挑选后三名学生;余下的不超过一名教师也不可能挑选后三名学生,矛盾。
下面先证明:对于互不相同的有序实数列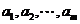 ,当
,当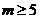 时,一定存在三个数
时,一定存在三个数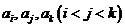 满足
满足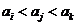 或
或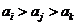 。
。
设最大数和最小数分别为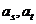 ,不妨假设
,不妨假设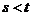 。若
。若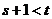 ,则
,则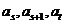 满足
满足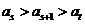 ;
;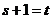 ,因为
,因为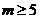 ,所以要么在
,所以要么在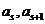 的前面,要么在
的前面,要么在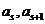 的后面至少有两个数,不妨假设在
的后面至少有两个数,不妨假设在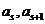 的后面有两个数
的后面有两个数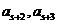 ,从而
,从而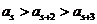 与
与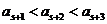 中一定有一个成立。
中一定有一个成立。
引用上面的结论,当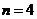 时,第一名教师至少可以挑选三名学生;若余下的学生大于等于
时,第一名教师至少可以挑选三名学生;若余下的学生大于等于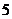 名,则第二名教师也至少可以挑选三名学生;这时剩下的学生的数目不超过
名,则第二名教师也至少可以挑选三名学生;这时剩下的学生的数目不超过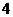 名,可以被两名教师全部挑选,因此,
名,可以被两名教师全部挑选,因此,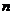 的最小值为
的最小值为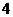 。
。
14.已知数列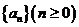 满足
满足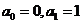 ,对于所有正整数
,对于所有正整数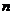 ,有
,有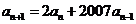 ,求使得
,求使得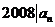 成立的最小正整数
成立的最小正整数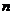 。
。
解法一 设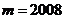 ,
,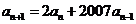 的特征方程为
的特征方程为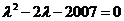 ,特征根为
,特征根为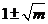 ,结合
,结合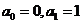 ,得
,得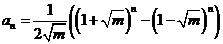 。由二项式定理得
。由二项式定理得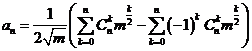 。
。
当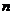 为奇数时,
为奇数时,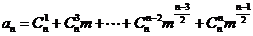 ;
;
当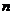 为偶数时,
为偶数时,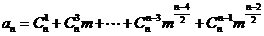 。
。
于是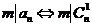 ,即
,即 ,所以满足条件的最小正整数为
,所以满足条件的最小正整数为 。
。
解法二 下面都是在模 意义下的
意义下的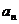 ,则
,则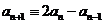 ,即
,即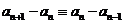 ,因此数列
,因此数列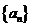 在模
在模 意义下具有等差数列的特点。又因为
意义下具有等差数列的特点。又因为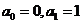 ,所以
,所以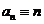 。于是有
。于是有 ,因此满足条件的最小正整数为
,因此满足条件的最小正整数为 。
。
13.已知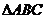 的外心为
的外心为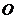 ,
,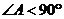 ,
,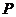 为
为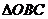 的外接圆上且在
的外接圆上且在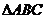 内部的任意一点,以
内部的任意一点,以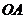 为直径的圆分别与
为直径的圆分别与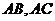 交于点
交于点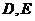 ,
, 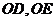 分别与
分别与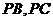 或其延长线交于点
或其延长线交于点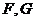 ,求证
,求证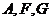 三点共线。
三点共线。
证明 连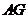 ,与
,与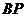 交于点
交于点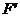 ,由于
,由于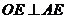 ,因此
,因此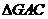 是等腰三角形,所以
是等腰三角形,所以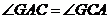 ,
,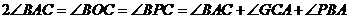 ,于是可得
,于是可得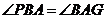 ,从而有
,从而有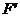 在
在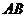 的中垂线上。由于
的中垂线上。由于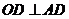 ,
,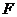 在
在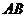 的中垂线上,于是有
的中垂线上,于是有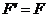 ,即
,即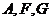 三点共线。
三点共线。
12.在平面直角坐标系中定义两点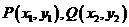 之间的交通距离为
之间的交通距离为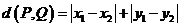 。若
。若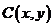 到点
到点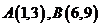 的交通距离相等,其中实数
的交通距离相等,其中实数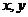 满足
满足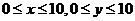 ,则所有满足条件的点
,则所有满足条件的点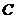 的轨迹的长之和为
。
的轨迹的长之和为
。
答 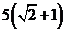 。
。
由条件得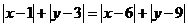 。
。
当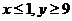 时,无解;
时,无解;
当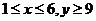 时,无解;
时,无解;
当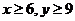 时,无解;
时,无解;
当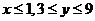 时,
时,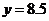 ,线段长为
,线段长为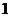 。
。
当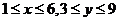 时,
时,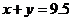 ,线段长为
,线段长为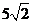 。
。
当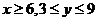 时
时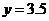 ,线段长为
,线段长为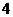 。
。
当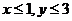 时,无解。
时,无解。
当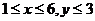 时,无解。
时,无解。
当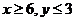 时,无解。
时,无解。
综上所述,点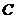 的轨迹构成的线段的长之和为
的轨迹构成的线段的长之和为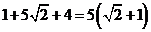 。
。
11.设集合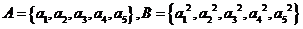 ,其中
,其中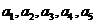 是五个不同的正整数,
是五个不同的正整数,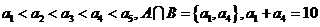 ,若
,若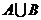 中所有元素的和为
中所有元素的和为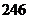 ,则满足条件的集合
,则满足条件的集合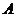 的个数为
。
的个数为
。
答 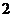 。
。
因为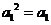 ,所以
,所以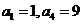 。由于
。由于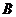 中有
中有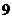 ,因此
,因此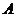 中有
中有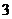 。若
。若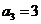 ,则
,则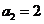 ,于是
,于是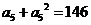 ,无正整数解。若
,无正整数解。若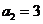 ,由于
,由于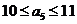 ,所以
,所以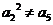 ,于是
,于是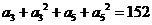 。又因为
。又因为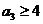 ,当
,当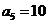 时,
时,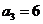 ;当
;当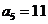 时,
时,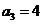 ,因此满足条件的
,因此满足条件的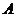 共有
共有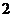 个,分别为
个,分别为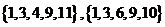 。
。
10.方程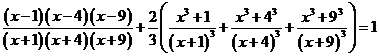 的不同非零整数解的个数为
。
的不同非零整数解的个数为
。
答 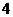 。
。
利用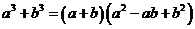 ,原方程
,原方程
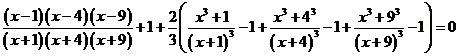
等价于
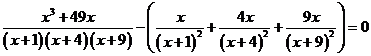 。
。
方程两端同除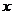 ,整理后得
,整理后得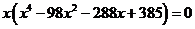 。再同除
。再同除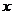 ,得
,得
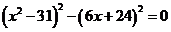 。
。
即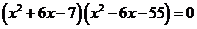 ,从而有
,从而有
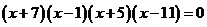 。
。
经验证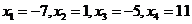 均是原方程的根,所以原方程共有
均是原方程的根,所以原方程共有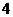 个整数根。
个整数根。
9.若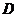 是边长为
是边长为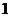 的正三角形
的正三角形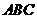 的边
的边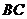 上的点,
上的点,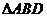 与
与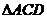 的内切圆半径分别为
的内切圆半径分别为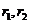 ,若
,若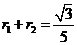 ,则满足条件的点
,则满足条件的点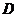 有两个,分别设为
有两个,分别设为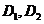 ,则
,则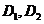 之间的距离为
。
之间的距离为
。
答 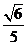 。
。
设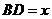 ,由余弦定理得
,由余弦定理得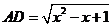 。一方面,
。一方面,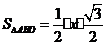 ,另一方面,
,另一方面,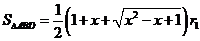 ,解得
,解得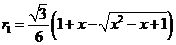 。同理可得
。同理可得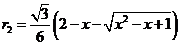 。从而有
。从而有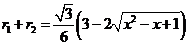 。当
。当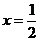 时,
时,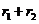 有最大值,且最大值为
有最大值,且最大值为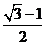 ,所以
,所以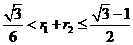 。由于
。由于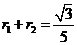 ,所以
,所以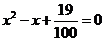 。设两个根分别为
。设两个根分别为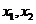 ,则
,则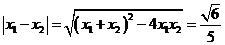 。
。
8.方程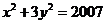 的所有正整数解为
。
的所有正整数解为
。
答 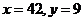 。
。
因为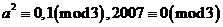 ,所以
,所以 。设
。设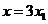 ,类似的可得
,类似的可得  。设
。设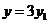 ,则原方程化为
,则原方程化为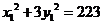 ,
,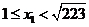 ,即
,即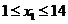 。因为
。因为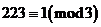 ,所以
,所以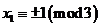 。又因为
。又因为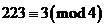 ,所以
,所以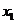 为偶数,于是
为偶数,于是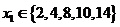 ,经验证,
,经验证,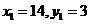 ,所以
,所以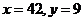 。
。
或由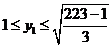 ,得
,得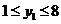 ,又因为
,又因为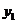 为奇数,所以经验证
为奇数,所以经验证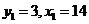 。
。
7.若关于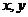 的方程组
的方程组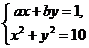 有解,且所有的解都是整数,则有序数对
有解,且所有的解都是整数,则有序数对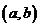 的数目为
。
的数目为
。
答 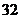 。
。
因为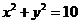 的整数解为
的整数解为
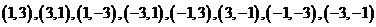 ,
,
所以这八个点两两所连的不过原点的直线有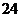 条,过这八个点的切线有
条,过这八个点的切线有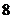 条,每条直线确定了唯一的有序数对
条,每条直线确定了唯一的有序数对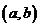 ,所以有序数对
,所以有序数对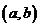 的数目为
的数目为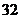 。
。
6.过四面体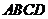 的顶点
的顶点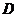 作半径为
作半径为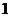 的球,该球与四面体
的球,该球与四面体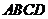 的外接球相切于点
的外接球相切于点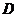 ,且与平面
,且与平面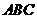 相切。若
相切。若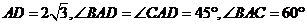 ,则四面体
,则四面体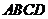 的外接球的半径
的外接球的半径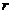 为(
)。
为(
)。
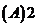
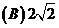
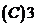
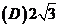
答 选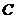 。
。
过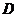 作平面
作平面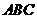 的垂线,垂足为
的垂线,垂足为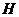 ,作
,作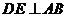 ,垂足为
,垂足为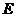 ,
,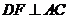 ,垂足为
,垂足为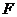 ,则
,则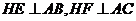 ,且有
,且有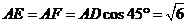 。由于
。由于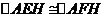 ,则
,则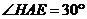 ,
,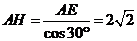 ,
,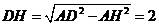 ,因此
,因此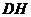 为半径为
为半径为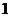 的球的直径,从而四面体
的球的直径,从而四面体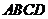 的外接球的球心
的外接球的球心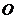 在
在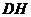 的延长线上,于是有
的延长线上,于是有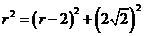 ,解得
,解得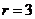 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com