
4.方程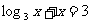 的解所在区间是( )
的解所在区间是( )
A.(0,2) B。(1,2) C.(2,3) D.(3,4)
3.函数f(x)的定义域为R,且x≠1,已知f(x+1)为奇函数,当x<1时,f(x)=2x2–x+1,那么当x>1时,f(x)的递减区间是 ( )
A.[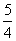 ,+∞
,+∞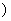 B.(1,
B.(1,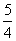
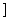 C.[
C.[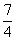 ,+∞
,+∞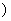 D.(1,
D.(1,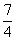 ]
]
2.已知函数f(x)=loga[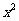 –(2a)2]对任意x∈[1,+∞]都有意义,则实数a的取值范围是
A.(0,
–(2a)2]对任意x∈[1,+∞]都有意义,则实数a的取值范围是
A.(0,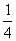
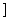 B.(0,
B.(0,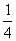 )
C.[
)
C.[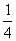 ,1
,1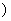 D.(
D.(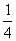 ,
,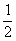 )
( )
)
( )
1.设函数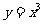 与
与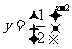 的图象的交点为
的图象的交点为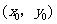 ,则
,则 所在的区间是 ( )
所在的区间是 ( )
A.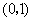 B.
B.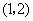 C.
C.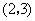 D.
D.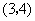
5.(07北京)对于函数①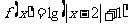 ,②
,②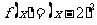 ,③
,③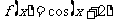 .判断如下三个命题的真假:命题甲:
.判断如下三个命题的真假:命题甲: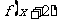 是偶函数;命题乙:
是偶函数;命题乙: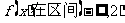 上是减函数,在区间
上是减函数,在区间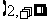 上是增函数;命题丙:
上是增函数;命题丙: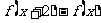 在
在 上是增函数.能使命题甲、乙、丙均为真的所有函数的序号是( )
上是增函数.能使命题甲、乙、丙均为真的所有函数的序号是( )
A.①③ B.①② C. ③ D. ②
函数的应用(2)作业
4.(07安徽)若对任意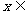 R,不等式
R,不等式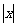 ≥ax恒成立,则实数a的取值范围是( )
≥ax恒成立,则实数a的取值范围是( )
A. a<-1
B.  ≤1
C.
≤1
C. <1
D.a≥1
<1
D.a≥1
3.设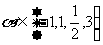 ,则使函数
,则使函数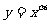 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有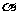 的值为( )
的值为( )
A.1,3 B.-1,1 C.-1,3 D.-1,1,3
2.(07重庆)已知定义域为R的函数 在区间
在区间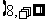 上为减函数,且函数
上为减函数,且函数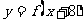 为偶函数,则( )
为偶函数,则( )
A.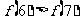 B.
B. 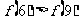 C.
C. 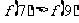 D.
D. 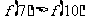
1.(07福建)已知函数 为R上的减函数,则满足
为R上的减函数,则满足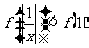 的实数
的实数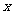 的取值范围是
的取值范围是
( ) A.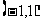 B.
B. C.
C.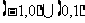 D.
D.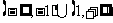
4.对于满足O≤p≤4的实数p,使x2+px>4x+p-3恒成立的x的取值范围是_____ __.
[典型例题]:
例1:已知函数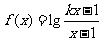 ,(k>0),
,(k>0),
(1)求函数f(x)的定义域;
(2)若函数f(x)在区间[10,+∞)上是增函数,求实数k的取值范围。
(1)当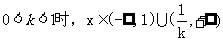 ,
,
当k=1时,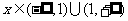
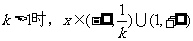
(2)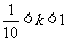
例2:.若函数f(x)对定义域中任意x均满足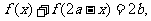 则称函数
则称函数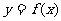 的图象关于点(a,b)对称.
的图象关于点(a,b)对称.
(1)已知函数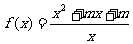 的图象关于点(0,1)对称,求实数m的值;
的图象关于点(0,1)对称,求实数m的值;
(2)已知函数g(x)在(-∞,0)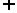 (0,+∞)上的图象关于点(0,1)对称,且当x∈(0,+∞)时,
(0,+∞)上的图象关于点(0,1)对称,且当x∈(0,+∞)时,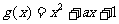 ,求函数g(x)在(-∞,0)上的解析式;
,求函数g(x)在(-∞,0)上的解析式;
(3)在(1)、(2)的条件下,当t>0时,若对实数任意x∈(-∞,0),恒有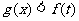 成立,求实数a的取值范围.
成立,求实数a的取值范围.
例3:已知二次函数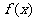 的二次项系数为
的二次项系数为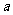 ,且不等式
,且不等式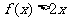 的解集为
的解集为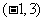 .
.
(1)若方程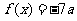 有两个相等的实数根,求
有两个相等的实数根,求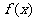 的解析式;
的解析式;
(2)若函数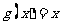
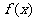 在区间
在区间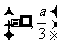 内单调递减,求
内单调递减,求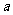 的取值范围;
的取值范围;
解:(1)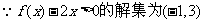 ,∴可设
,∴可设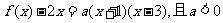 ,
,
因而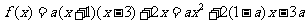 ①
①
由 得
得 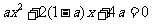 ②
②
∵方程②有两个相等的根,∴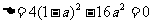 ,即
,即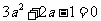 解得
解得 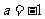 或
或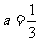 由于
由于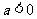 ,
,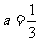 (舍去),将
(舍去),将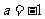 代入 ① 得
代入 ① 得
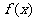 的解析式
的解析式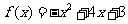 .
.
(2)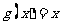
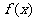 =
= ,∵
,∵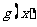 在区间
在区间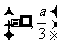 内单调递减,
内单调递减,
∴ 在
在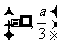 上的函数值非正,
上的函数值非正,
由于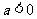 ,对称轴
,对称轴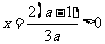 ,故只需
,故只需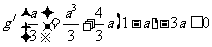 ,注意到
,注意到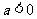 ,∴
,∴ ,得
,得 或
或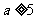 (舍去)
(舍去)
故所求a的取值范围是 .
.
例4:已知函数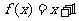 ,设
,设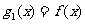 ,
,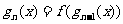
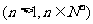
(1)求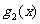 ,
,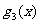 的表达式,并猜想
的表达式,并猜想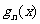
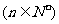 的表达式(直接写出猜想结果)
的表达式(直接写出猜想结果)
(2)若关于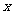 的函数
的函数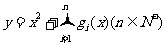 在区间
在区间 上的最小值为6,求
上的最小值为6,求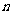 的值。
的值。
(1)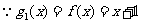 ,
,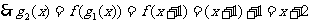
 ,
,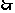 猜想
猜想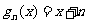
(2)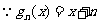 ,
,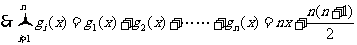
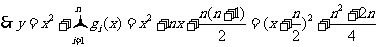
(1)当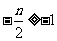 ,即
,即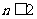 时,函数
时,函数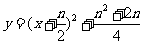 在区间
在区间 上是减函数
上是减函数
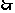 当
当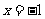 时,
时,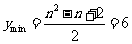 ,即
,即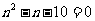 ,该方程没有整数解
,该方程没有整数解
(2)当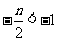 ,即
,即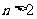 时,
时, ,解得
,解得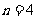 ,综上所述,
,综上所述,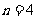
[命题展望]:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com