
1.(2008山东)函数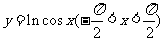 的图象是
( )
的图象是
( )
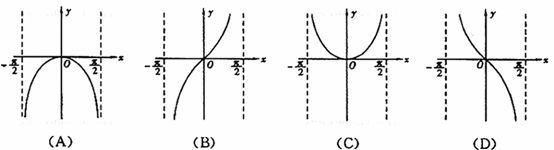
答案:A
解析 本题考查复合函数的图象。
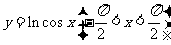 是偶函数,可排除B,D; 由
是偶函数,可排除B,D; 由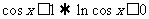 排除C,选A
排除C,选A
43.(2009上海卷文)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分 .
已知ΔABC的角A、B、C所对的边分别是a、b、c,设向量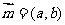 ,
,
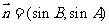 ,
, .
.
(1)
若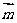 //
//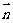 ,求证:ΔABC为等腰三角形;
,求证:ΔABC为等腰三角形;
(2)
若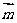 ⊥
⊥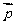 ,边长c = 2,角C =
,边长c = 2,角C = 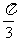 ,求ΔABC的面积 .
,求ΔABC的面积 .
证明:(1)
即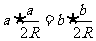 ,其中R是三角形ABC外接圆半径,
,其中R是三角形ABC外接圆半径,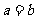


 为等腰三角形
为等腰三角形
解(2)由题意可知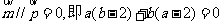
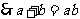
由余弦定理可知, 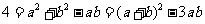






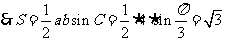
w
2005--2008年高考题
42.(2009重庆卷理)(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分.)
设函数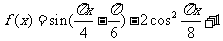 .
.
(Ⅰ)求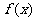 的最小正周期.
的最小正周期.


(Ⅱ)若函数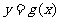 与
与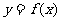 的图像关于直线
的图像关于直线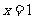 对称,求当
对称,求当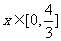 时
时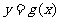 的最大值.
的最大值.
解:(Ⅰ)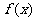 =
=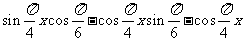
=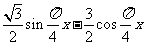
=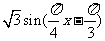


故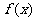 的最小正周期为T =
的最小正周期为T = 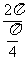 =8
=8
(Ⅱ)解法一:
在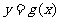 的图象上任取一点
的图象上任取一点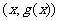 ,它关于
,它关于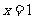 的对称点
的对称点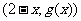 .
.
由题设条件,点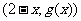 在
在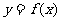 的图象上,从而
的图象上,从而 

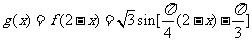
=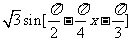
=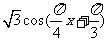
当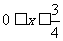 时,
时,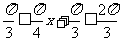 ,因此
,因此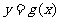 在区间
在区间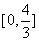 上的最大值为
上的最大值为
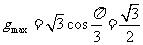


解法二:
因区间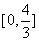 关于x = 1的对称区间为
关于x = 1的对称区间为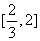 ,且
,且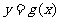 与
与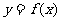 的图象关于
的图象关于
x = 1对称,故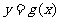 在
在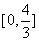 上的最大值为
上的最大值为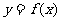 在
在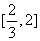 上的最大值
上的最大值
由(Ⅰ)知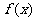 =
=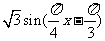
当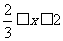 时,
时,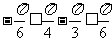
因此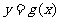 在
在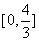 上的最大值为
上的最大值为 

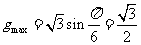
. 42.(2009重庆卷文)(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分.)
设函数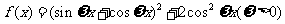 的最小正周期为
的最小正周期为 .
.
(Ⅰ)求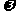 的最小正周期.
的最小正周期.
(Ⅱ)若函数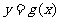 的图像是由
的图像是由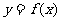 的图像向右平移
的图像向右平移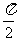 个单位长度得到,求
个单位长度得到,求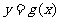 的单调增区间.
的单调增区间.
解:(Ⅰ)
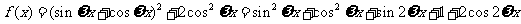
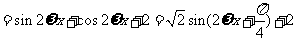
依题意得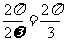 ,故
,故 的最小正周期为
的最小正周期为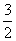 .
. 

(Ⅱ)依题意得: 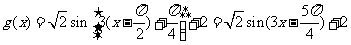
由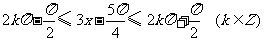
解得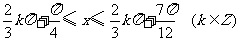 \
\ 

故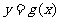 的单调增区间为:
的单调增区间为: 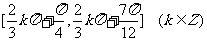
41.(2009福建卷文).c.o.m 
 已知函数
已知函数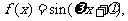 其中
其中 ,
,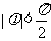
(I)若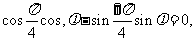 求
求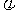 的值;
的值;


(Ⅱ)在(I)的条件下,若函数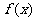 的图像的相邻两条对称轴之间的距离等于
的图像的相邻两条对称轴之间的距离等于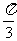 ,求函数
,求函数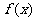 的解析式;并求最小正实数
的解析式;并求最小正实数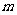 ,使得函数
,使得函数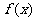 的图像象左平移
的图像象左平移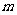 个单位所对应的函数是偶函数。
个单位所对应的函数是偶函数。
解法一:
(I)
由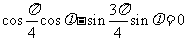 得
得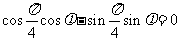
即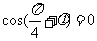 又
又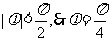


(Ⅱ)由(I)得,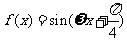
依题意,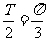
又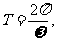
故函数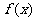 的图像向左平移
的图像向左平移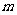 个单位后所对应的函数为
个单位后所对应的函数为
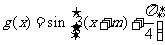
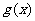 是偶函数当且仅当
是偶函数当且仅当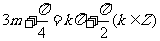
即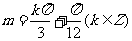
从而,最小正实数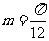
解法二:
(I)同解法一
(Ⅱ)由(I)得,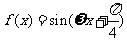

依题意,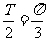


又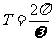 ,故
,故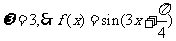
函数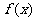 的图像向左平移
的图像向左平移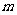 个单位后所对应的函数为
个单位后所对应的函数为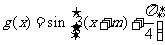
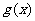 是偶函数当且仅当
是偶函数当且仅当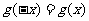 对
对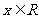 恒成立
恒成立
亦即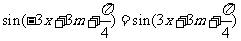 对
对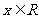 恒成立。
恒成立。
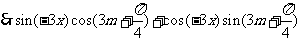
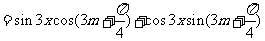
即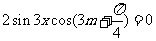 对
对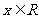 恒成立。
恒成立。
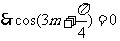
故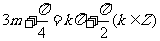
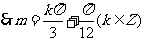


从而,最小正实数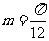
40.(2009湖南卷理)在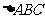 ,已知
,已知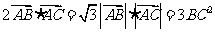 ,求角A,B,C的大小.
,求角A,B,C的大小.
解:设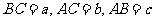
由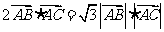 得
得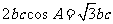 ,所以
,所以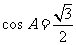
又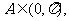 因此
因此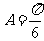


由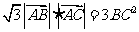 得
得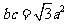 ,于是
,于是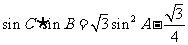
所以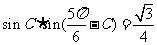 ,
,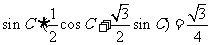 ,因此
,因此
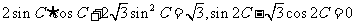 ,既
,既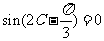
由A=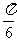 知
知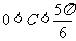 ,所以
,所以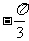 ,
,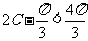 ,从而
,从而
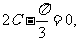 或
或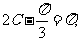 ,既
,既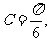 或
或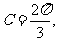 故
故
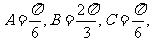 或
或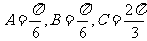
40.(2009湖北卷文) 在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且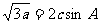
(Ⅰ)确定角C的大小: 

(Ⅱ)若c=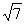 ,且△ABC的面积为
,且△ABC的面积为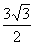
 ,求a+b的值。
,求a+b的值。
解(1)由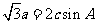 及正弦定理得,
及正弦定理得,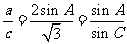


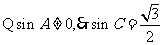
 是锐角三角形,
是锐角三角形,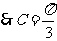
(2)解法1: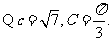 由面积公式得
由面积公式得
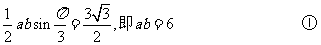
由余弦定理得 

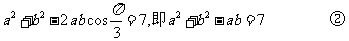
由②变形得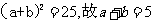
解法2:前同解法1,联立①、②得
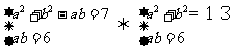
消去b并整理得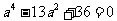 解得
解得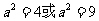
所以 故
故


39.(2009陕西卷理)(本小题满分12分)
已知函数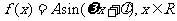 (其中
(其中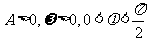 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为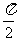 ,且图象上一个最低点为
,且图象上一个最低点为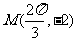 .
.
(Ⅰ)求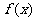 的解析式;(Ⅱ)当
的解析式;(Ⅱ)当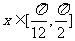 ,求
,求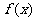 的值域.
的值域.
解(1)由最低点为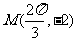 得A=2.
得A=2.
由x轴上相邻的两个交点之间的距离为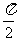 得
得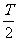 =
=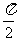 ,即
,即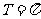 ,
,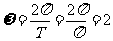
由点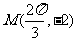 在图像上的
在图像上的
故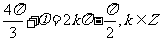
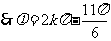


又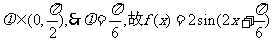
(2)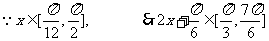

当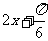 =
=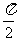 ,即
,即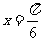 时,
时,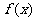 取得最大值2;当
取得最大值2;当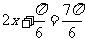
即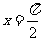 时,
时,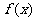 取得最小值-1,故
取得最小值-1,故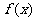 的值域为[-1,2]
的值域为[-1,2] 

38.(2009全国卷Ⅱ理)设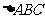 的内角
的内角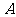 、
、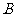 、
、 的对边长分别为
的对边长分别为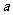 、
、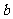 、
、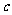 ,
,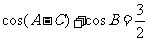 ,
,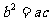 ,求
,求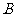 。
。
分析:由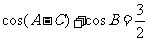 ,易想到先将
,易想到先将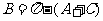 代入
代入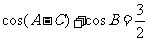 得
得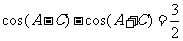 。然后利用两角和与差的余弦公式展开得
。然后利用两角和与差的余弦公式展开得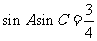 ;又由
;又由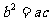 ,利用正弦定理进行边角互化,得
,利用正弦定理进行边角互化,得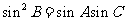 ,进而得
,进而得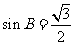 .故
.故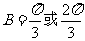 。大部分考生做到这里忽略了检验,事实上,当
。大部分考生做到这里忽略了检验,事实上,当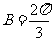 时,由
时,由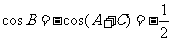 ,进而得
,进而得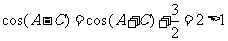 ,矛盾,应舍去。
,矛盾,应舍去。
也可利用若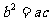 则
则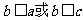 从而舍去
从而舍去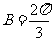 。不过这种方法学生不易想到。
。不过这种方法学生不易想到。
评析:本小题考生得分易,但得满分难。
37.(2009江西卷理)△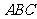 中,
中,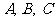 所对的边分别为
所对的边分别为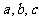 ,
,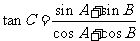 ,
,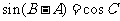 .
.
(1)求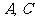 ;
;
(2)若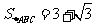 ,求
,求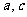 .
. 

解:(1) 因为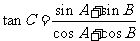 ,即
,即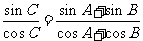 ,
,
所以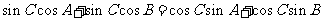 ,
,
即 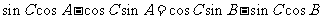 ,
,
得 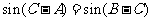 . 所以
. 所以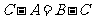 ,或
,或 (不成立).
(不成立).
即 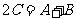 , 得
, 得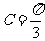 ,所以.
,所以.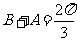
又因为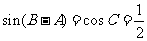 ,则
,则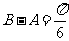 ,或
,或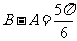 (舍去)
(舍去)
得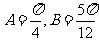
(2)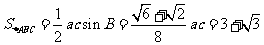 ,
,
又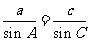 , 即
, 即 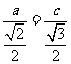 ,
, 

得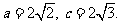
36.(2009江西卷文)(本小题满分12分)
在△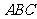 中,
中,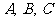 所对的边分别为
所对的边分别为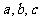 ,
,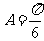 ,
,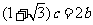 .
.
(1)求 ;
;
(2)若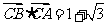 ,求
,求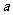 ,
,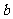 ,
,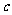 .
.
解:(1)由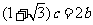 得
得 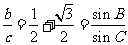
则有 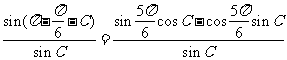 =
=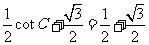
得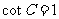 即
即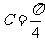 .
.
(2) 由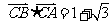 推出
推出 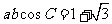 ;而
;而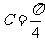 ,
,
即得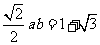 ,
,
则有  解得
解得 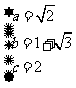
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com