
(二)了解正弦、余弦、正切函数的图象的画法,会用“五点法”画正弦、余弦函数和函数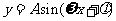 的简图,并能由图象写出解析式.
的简图,并能由图象写出解析式.
⑴“五点法”作图的列表方式;
⑵求解析式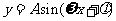 时处相
时处相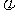 的确定方法:代(最高、低)点法、公式
的确定方法:代(最高、低)点法、公式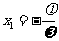 .
.
(一)列表综合三个三角函数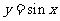 ,
,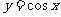 ,
,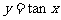 的图象与性质,并挖掘:
的图象与性质,并挖掘:
⑴最值的情况;
⑵了解周期函数和最小正周期的意义.会求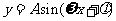 的周期,或者经过简单的恒等变形可化为上述函数的三角函数的周期,了解加了绝对值后的周期情况;
的周期,或者经过简单的恒等变形可化为上述函数的三角函数的周期,了解加了绝对值后的周期情况;
⑶会从图象归纳对称轴和对称中心;
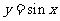 的对称轴是
的对称轴是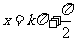
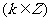 ,对称中心是
,对称中心是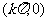
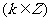 ;
;
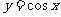 的对称轴是
的对称轴是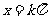
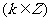 ,对称中心是
,对称中心是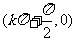
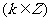
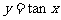 的对称中心是
的对称中心是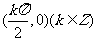
注意加了绝对值后的情况变化.
⑷写单调区间注意 .
.
1、终边相同的角的表示方法:凡是与终边α相同的角,都可以表示成k·3600+α的形式,特例,终边在x轴上的角集合{α|α=k·1800,k∈Z},终边在y轴上的角集合{α|α=k·1800+900,k∈Z},终边在坐标轴上的角的集合{α|α=k·900,k∈Z}。在已知三角函数值的大小求角的大小时,通常先确定角的终边位置,然后再确定大小。
理解弧度的意义,并能正确进行弧度和角度的换算;
⑴角度制与弧度制的互化: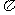 弧度
弧度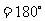 ,
,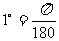 弧度,
弧度,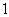 弧度
弧度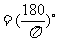
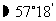
⑵弧长公式: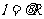 ;扇形面积公式:
;扇形面积公式: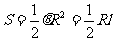 。
。
2、任意角的三角函数的定义、三角函数的符号规律、特殊角的三角函数值、同角三角函数的关系式、诱导公式:
(1)三角函数定义:角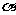 中边上任意一点
中边上任意一点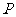 为
为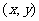 ,设
,设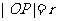 则:
则:
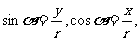
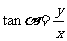
(2)三角函数符号规律:一全正,二正弦,三正切,四余弦;
(3)特殊角的三角函数值
|
α |
0 |
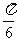 |
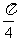 |
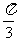 |
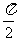 |
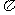 |
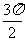 |
2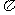 |
|
sinα |
0 |
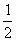 |
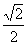 |
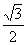 |
1 |
0 |
-1 |
0 |
|
cosα |
1 |
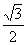 |
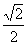 |
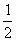 |
0 |
-1 |
0 |
1 |
|
tanα |
0 |
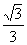 |
1 |
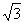 |
不存在 |
0 |
不存在 |
0 |
(3)同角三角函数的基本关系: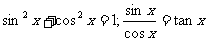
(4)诱导公式(奇变偶不变,符号看象限):
sin( )=sinα,cos(
)=sinα,cos( )=-cosα,tan(
)=-cosα,tan( )=-tanα
)=-tanα
sin( )=-sinα,cos(
)=-sinα,cos( )=-cosα,tan(
)=-cosα,tan( )=tanα
)=tanα
sin( )=-sinα,cos(
)=-sinα,cos( )=cosα,tan(
)=cosα,tan( )=-tanα
)=-tanα
sin( )=-sinα,cos(
)=-sinα,cos( )=cosα,tan(
)=cosα,tan( )=-tanα
)=-tanα
sin( )=sinα,cos(
)=sinα,cos( )=cosα,tan(
)=cosα,tan( )=tanα,
)=tanα,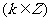
sin(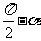 )=cosα,cos(
)=cosα,cos(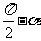 )=sinα
)=sinα
sin(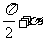 )=cosα,cos(
)=cosα,cos(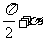 )=-sinα
)=-sinα
3、两角和与差的三角函数
(1)和(差)角公式
①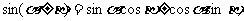
②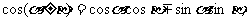 ③
③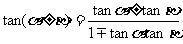
(2)二倍角公式
二倍角公式:①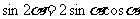 ;
;
②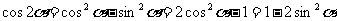 ;③
;③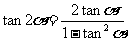
(3)经常使用的公式
①升(降)幂公式: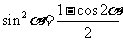 、
、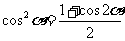 、
、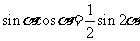 ;
;
②辅助角公式: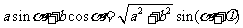 (
(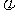 由
由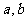 具体的值确定);
具体的值确定);
③正切公式的变形: .
.
4、三角函数的图象与性质
7.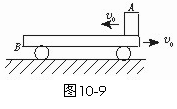 (★★★★★)如图10-9所示,一质量为M的平板车B放在光滑水平面上,在其右端放一质量为m的小木块A,m<M,A、B间动摩擦因数为μ,现给A和B以大小相等、方向相反的初速度v0,使A开始向左运动,B开始向右运动,最后A不会滑离B,求:
(★★★★★)如图10-9所示,一质量为M的平板车B放在光滑水平面上,在其右端放一质量为m的小木块A,m<M,A、B间动摩擦因数为μ,现给A和B以大小相等、方向相反的初速度v0,使A开始向左运动,B开始向右运动,最后A不会滑离B,求:
(1)A、B最后的速度大小和方向.
(2)从地面上看,小木块向左运动到离出发点最远处时,平板车向右运动的位移大小.
6.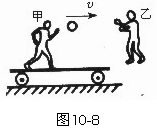 (★★★★★)如图10-8所示甲、乙两人做抛球游戏,甲站在一辆平板车上,车与水平地面间摩擦不计.甲与车的总质量M=100 kg,另有一质量m=2
kg的球.乙站在车的对面的地上,身旁有若干质量不等的球.开始车静止,甲将球以速度v(相对地面)水平抛给乙,乙接到抛来的球后,马上将另一质量为m′=2m的球以相同速率v水平抛回给甲,甲接住后,再以相同速率v将此球水平抛给乙,这样往复进行.乙每次抛回给甲的球的质量都等于他接到的球的质量为2倍,求:
(★★★★★)如图10-8所示甲、乙两人做抛球游戏,甲站在一辆平板车上,车与水平地面间摩擦不计.甲与车的总质量M=100 kg,另有一质量m=2
kg的球.乙站在车的对面的地上,身旁有若干质量不等的球.开始车静止,甲将球以速度v(相对地面)水平抛给乙,乙接到抛来的球后,马上将另一质量为m′=2m的球以相同速率v水平抛回给甲,甲接住后,再以相同速率v将此球水平抛给乙,这样往复进行.乙每次抛回给甲的球的质量都等于他接到的球的质量为2倍,求:
(1)甲第二次抛出球后,车的速度大小.
(2)从第一次算起,甲抛出多少个球后,再不能接到乙抛回来的球.
5.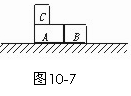 (★★★★★)如图10-7所示,在光滑水平面上有两个并排放置的木块A和B,已知mA=0.5 kg,mB=0.3 kg,有一质量为mC=0.1 kg的小物块C以20 m/s的水平速度滑上A表面,由于C和A、B间有摩擦,C滑到B表面上时最终与B以2.5 m/s的共同速度运动,求:
(★★★★★)如图10-7所示,在光滑水平面上有两个并排放置的木块A和B,已知mA=0.5 kg,mB=0.3 kg,有一质量为mC=0.1 kg的小物块C以20 m/s的水平速度滑上A表面,由于C和A、B间有摩擦,C滑到B表面上时最终与B以2.5 m/s的共同速度运动,求:
(1)木块A的最后速度.
(2)C离开A时C的速度.
4.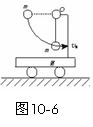 (★★★★)质量为M的小车静止在光滑的水平面上,质量为m的小球用细绳吊在小车上O点,将小球拉至水平位置A点静止开始释放(如图10-6所示),求小球落至最低点时速度多大?(相对地的速度)
(★★★★)质量为M的小车静止在光滑的水平面上,质量为m的小球用细绳吊在小车上O点,将小球拉至水平位置A点静止开始释放(如图10-6所示),求小球落至最低点时速度多大?(相对地的速度)
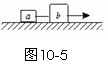
3.(★★★★)如图10-5所示,质量分别为m和M的铁块a和b用细线相连,在恒定的力作用下在水平桌面上以速度v匀速运动.现剪断两铁块间的连线,同时保持拉力不变,当铁块a停下的瞬间铁块b的速度大小为_______.
2.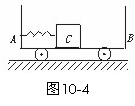 (★★★★)小车AB静置于光滑的水平面上,A端固定一个轻质弹簧,B端粘有橡皮泥,AB车质量为M,长为L,质量为m的木块C放在小车上,用细绳连结于小车的A端并使弹簧压缩,开始时AB与C都处于静止状态,如图10-4所示,当突然烧断细绳,弹簧被释放,使物体C离开弹簧向B端冲去,并跟B端橡皮泥粘在一起,以下说法中正确的是
(★★★★)小车AB静置于光滑的水平面上,A端固定一个轻质弹簧,B端粘有橡皮泥,AB车质量为M,长为L,质量为m的木块C放在小车上,用细绳连结于小车的A端并使弹簧压缩,开始时AB与C都处于静止状态,如图10-4所示,当突然烧断细绳,弹簧被释放,使物体C离开弹簧向B端冲去,并跟B端橡皮泥粘在一起,以下说法中正确的是
A.如果AB车内表面光滑,整个系统任何时刻机械能都守恒
B.整个系统任何时刻动量都守恒
C.当木块对地运动速度为v时,小车对地运动速度为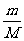 v
v
 D.AB车向左运动最大位移小于
D.AB车向左运动最大位移小于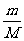 L
L
1.(★★★)质量相同的两个小球在光滑水平面上沿连心线同向运动,球1的动量为 7 kg·m/s,球2的动量为5 kg·m/s,当球1追上球2时发生碰撞,则碰撞后两球动量变化的可能值是
A.Δp1=-1 kg·m/s,Δp2=1 kg·m/s
B.Δp1=-1 kg·m/s,Δp2=4 kg·m/s
C.Δp1=-9 kg·m/s,Δp2=9 kg·m/s
D.Δp1=-12 kg·m/s,Δp2=10 kg·m/s
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com