
36.[2010·石家庄市教学质量检测(二)]过椭圆左焦点F且倾斜角为60 的直线交椭圆于A,B两点,若|FA|=
的直线交椭圆于A,B两点,若|FA|=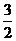 |FB|,则椭圆的离心率等于 ( )
|FB|,则椭圆的离心率等于 ( )
 A.
A.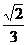 B.
B.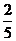 C.
C.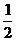 D.
D.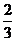
[答案]B
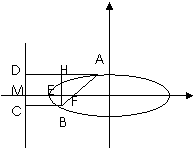
[解析]设作准线与x轴交点为M,过A、B准线的垂线,垂足分别为D、C,过B作BH⊥AD,垂足为H,交x轴于E。因为AB倾斜角为60 ,所以∠ABH=30
,所以∠ABH=30 ,设AB=5,因为|FA|=
,设AB=5,因为|FA|=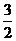 |FB|,则BF=2,AF=3,AH== =,所以e=
|FB|,则BF=2,AF=3,AH== =,所以e=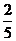 ,选择B。
,选择B。
35.[2010·泰安市第一轮复习质检]已知双曲线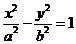 的一条渐近线方程为
的一条渐近线方程为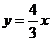 ,
则双曲线的离心率为( )
,
则双曲线的离心率为( )
A.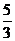 B.
B.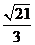 C.
C.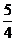 D.
D.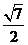
[答案]A
[解析]依题意,e=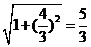 ,选择A。
,选择A。
34.[2010·重庆南开中学第八次月考]过双曲线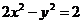 的右焦点作直线
的右焦点作直线 交双曲线于
交双曲线于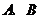 两点,若
两点,若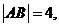 则这样的直线有( )
则这样的直线有( )
A.4条 B.3条 C.2条 D.1条
[答案]B
[解析]因为双曲线方程为x2-=1,过右焦点垂直于x轴的弦长,即通径为=4,又实轴长为2a=2<4,由对称性可知,过右焦点长度为4的弦与左右两支各有一个交点的弦有两条,与右支有两个交点的弦只有1条,故共有3条长度为4的弦。选B。
33.[2010·滦县一中]双曲线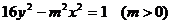 的一个顶点到它的一条渐近线的距离是
的一个顶点到它的一条渐近线的距离是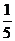 ,则
,则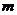 的值是( )
的值是( )
A.1 B.2 C.3 D.4
[答案]C
[解析]令x=0,得y=±,即双曲线的顶点坐标为(0, ±),又其渐近线方程为:y=±x,由点到直线的距离公式得:=,解得:m=3。
32.[2010·宣武一模]设圆 的圆心在双曲线
的圆心在双曲线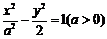 的右焦点且与此双曲线的渐近线相切,若圆
的右焦点且与此双曲线的渐近线相切,若圆 被直线
被直线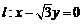 截得的弦长等于
截得的弦长等于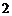 ,则
,则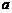 的值为( )
的值为( )
A.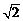 B.
B.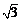 C.
C.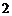 D.
D.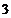
[答案]A
[解析]圆 的圆心
的圆心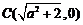 ,双曲线的渐近线方程为
,双曲线的渐近线方程为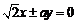 ,
, 到渐近线的距离为
到渐近线的距离为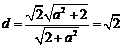 ,故圆
,故圆 方程
方程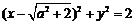 .由
.由 被圆
被圆 截得的弦长是
截得的弦长是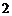 及圆
及圆 的半径为
的半径为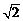 可知,圆心
可知,圆心 到直线
到直线 的距离为
的距离为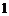 ,即
,即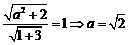 .
.
31.[2010·宣武一模]若椭圆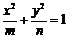 与双曲线
与双曲线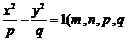 均为正数)有共同的焦点
均为正数)有共同的焦点 ,
, ,
,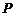 是两曲线的一个公共点,则
是两曲线的一个公共点,则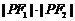 等于( )
等于( )
A.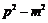 B.
B.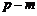 C.
C.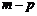 D.
D.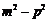
[答案]C
[解析]由题设可知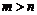 ,再由椭圆和双曲线的定义有
,再由椭圆和双曲线的定义有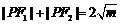 及
及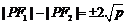 ,两个式子分别平方再相减即可得
,两个式子分别平方再相减即可得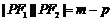 .选C。
.选C。
30.[2010·朝阳一模]已知点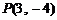 是双曲线
是双曲线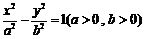 渐近线上的一点,
渐近线上的一点,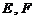 是左、右两个焦点,若
是左、右两个焦点,若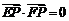 ,则双曲线方程为( )
,则双曲线方程为( )
A.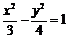 B.
B.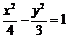 C.
C.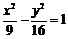 D.
D.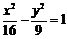
[答案]C
[解析]不妨设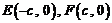 ,于是有
,于是有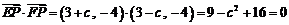 .
.
于是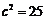 .排除A,B.又由D中双曲线的渐近线方程为
.排除A,B.又由D中双曲线的渐近线方程为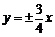 ,点
,点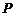 不在其上,排除D.
不在其上,排除D.
29.[2010·湖南师大附中第二次月考]已知曲线C的参数方程是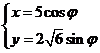 (
(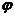 为参数),则曲线C上的点P到定点M(-2,0)的最大距离是 ( )
为参数),则曲线C上的点P到定点M(-2,0)的最大距离是 ( )
A.9 B. 8 C. 7 D. 6
[答案]C
[解析]解法一:因为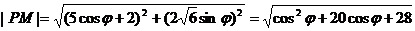
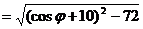 ,所以当
,所以当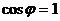 时,
时,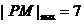 ,故选C.
,故选C.
解法二:将曲线C的参数方程化为普通方程,得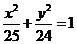 ,它表示焦点在x轴上的椭圆.由椭圆的几何性质可知,当点P位于椭圆的右顶点时,|PM|为最大,且最大值为5+2=7,故选C.
,它表示焦点在x轴上的椭圆.由椭圆的几何性质可知,当点P位于椭圆的右顶点时,|PM|为最大,且最大值为5+2=7,故选C.
28.[2010·曲靖一中届高考冲刺卷数学(六)]设F1,F2分别是椭圆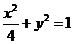 的左、右焦点,P是第一象限内该椭圆上的一点,且
的左、右焦点,P是第一象限内该椭圆上的一点,且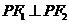 ,求点P的横坐标为( )
,求点P的横坐标为( )
A、1 B、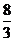 C、
C、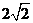 D、
D、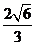
[答案]D
[解析]由题意半焦距c=,又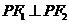 ,为此点P在以为半径,以原点为圆心的圆上,由解得P(,).故选D。
,为此点P在以为半径,以原点为圆心的圆上,由解得P(,).故选D。
27.[2010·江西省重点中学第二次联考]设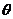 是△ABC的一个内角,且
是△ABC的一个内角,且 ,则
,则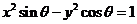 表示( )
表示( )
A.焦点在x轴上的椭圆 B.焦点在y轴上的椭圆
C.焦点在x轴上的双曲线 D.焦点在y轴上的双曲线
[答案]B
[解析]因为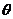 ∈(0,π),且
∈(0,π),且 ,所以
,所以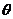 ∈(,π),且|sin
∈(,π),且|sin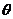 |>|cos
|>|cos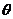 |,所以
|,所以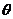 ∈(,),从而cos
∈(,),从而cos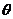 <0,从而
<0,从而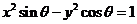 表示焦点在y轴上的椭圆。选B
表示焦点在y轴上的椭圆。选B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com