
2.二面角的平面角的定义、作法.
1.二面角的定义、画法.
3.设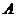 在平面
在平面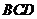 内的射影是直角三角形
内的射影是直角三角形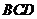 的斜边
的斜边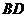 的中点
的中点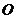 ,
,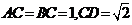 ,求(1)
,求(1)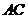 与平面
与平面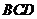 所成角的大小;(2)二面角
所成角的大小;(2)二面角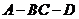 的大小;(3)异面直线
的大小;(3)异面直线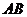 和
和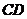 的大小
的大小
解:(1)∵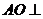 面
面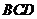 ∴
∴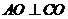
∴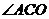 为
为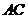 与面
与面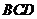 所成角
所成角
∵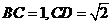 ∴
∴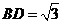
∴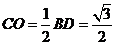 ∴
∴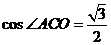
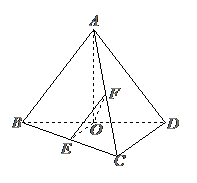 ∴
∴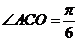
即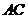 与平面
与平面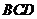 所成角的大小为
所成角的大小为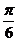

(2)取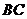 中点
中点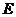 ,连接
,连接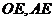 ∴
∴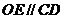
∵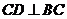 ∴
∴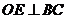
又∵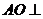 面
面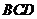 ∴
∴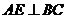
∴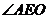 为二面角
为二面角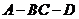 的平面角
的平面角
又∵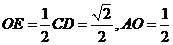
∵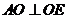 ∴
∴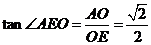 ∴
∴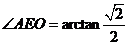
即二面角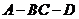 的大小为
的大小为

(3)取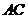 的中点
的中点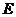 ,连接
,连接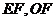 ,则
,则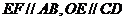
∴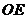 与
与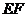 所成的锐角或直角即为异面直线
所成的锐角或直角即为异面直线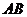 和
和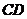 所成角
所成角
易求得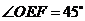

即异面直线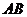 和
和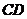 所成角为
所成角为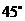

 1
1 ?如图所示,已知
?如图所示,已知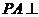 面
面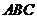 ,
,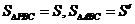 ,二面角
,二面角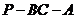 的平面角为
的平面角为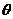 ,
,
求证: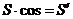
证明:过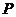 作
作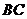 的垂线,垂足为
的垂线,垂足为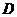 ,连接
,连接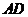
∵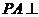 平面
平面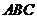 ,
,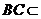 平面
平面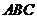 ,
,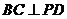
∴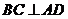
∴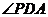 为二面角
为二面角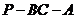 的平面角,
的平面角,
即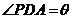
∵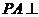 面
面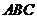 ∴
∴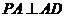
∵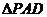 是直角三角形 ∴
是直角三角形 ∴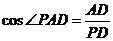
又∵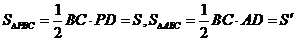
∴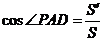 ∴
∴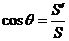 即
即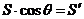
说明:这是推广的射影定理,也是求二面角平面角的一种方法
2.如图,在空间四边形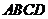 中,
中,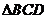 是正三角形,
是正三角形,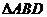 是等腰直角三角形,且
是等腰直角三角形,且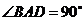 ,又二面角
,又二面角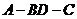 为直二面角,求二面角
为直二面角,求二面角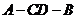 的大小
的大小
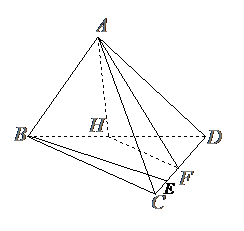 解:过
解:过 作
作 于
于
∵二面角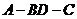 为直二面角 ∴
为直二面角 ∴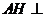 面
面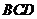
取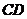 中点
中点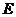 ,
,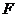 为
为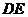 中点,连接
中点,连接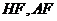
∵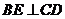 ∴
∴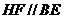
∴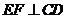 ∴
∴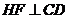
∴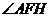 为二面角
为二面角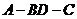 的平面角
的平面角
令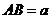 ,则
,则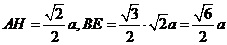
∴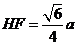 ∴在
∴在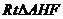 中
中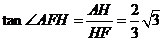
∴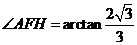
即二面角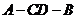 的大小为
的大小为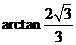

例1  在正四面体
在正四面体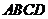 中,求相邻两个平面所成的二面角的平面角的大小
中,求相邻两个平面所成的二面角的平面角的大小
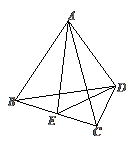 解:取
解:取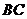 的中点
的中点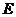 ,连接
,连接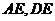 ,
,
∵正四面体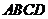 ,∴
,∴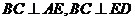 于
于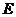 ,
,
∴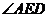 为二面角
为二面角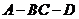 的平面角,
的平面角,
方法一:设正四面体的棱长为1,
则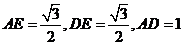 ,由余弦定理得
,由余弦定理得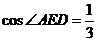
方法二:(向量运算)令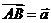 ,
,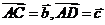 ,棱长为1,
,棱长为1,
∵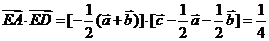 ,
,
又∵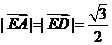 ,∴
,∴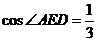
即相邻两个平面所成的二面角的平面角的大小为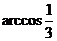 .
.
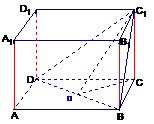
例2.在棱长为1的正方体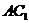 中,
中,
(1)求二面角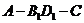 的大小;
的大小;
(2)求平面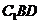 与底面
与底面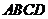 所成二面角
所成二面角 的平面角大小
的平面角大小
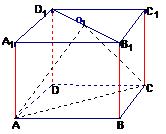 解:(1)取
解:(1)取 中点
中点 ,连接
,连接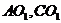 ,
,
∵正方体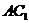 ,∴
,∴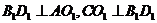 ,
,
∴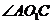 即为二面角
即为二面角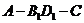 的平面角,
的平面角,
在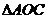 中,
中,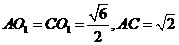 ,
,
可以求得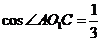 即二面角
即二面角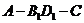 的大小为
的大小为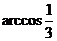 .
.
 (2)过
(2)过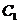 作
作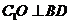 于点
于点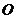 ,
,
∵正方体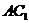 ,∴
,∴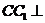 平面
平面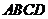 ,
,
∴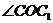 为平面
为平面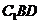 与平面
与平面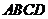 所成二面角
所成二面角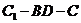 的平面角,
的平面角,
可以求得: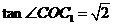
所以,平面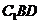 与底面
与底面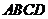 所成二面角
所成二面角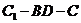 的平面角大小为
的平面角大小为 .
.
说明:求二面角的步骤:作--证--算--答
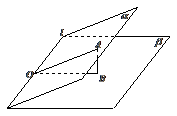 例3.已知:二面角
例3.已知:二面角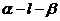 且
且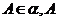 到平面
到平面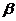 的距离为
的距离为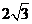 ,
,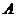 到
到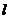 的距离为
的距离为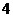 ,求二面角
,求二面角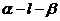 的大小
的大小
解:作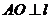 于点
于点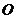 ,
,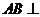 平面
平面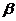 于点
于点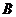 ,连接
,连接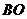 ,
,
∵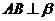 于点
于点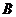 ,
,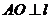 于点
于点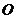 ,
,
∴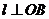 ,∴
,∴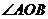 即为二面角
即为二面角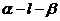 的平面角,
的平面角,
易知,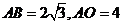 ,
,
∴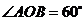 即二面角
即二面角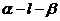 的大小为
的大小为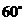 .
.
说明:利用三垂线定理作二面角的平面角是解决二面角问题中一种重要的方法,其特征是其中一个平面内一点作另一个平面的垂线 则已经有三种作二面角的平面角的方法,即:定义法、垂面法、三垂线法
则已经有三种作二面角的平面角的方法,即:定义法、垂面法、三垂线法
例4.如图,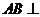 平面
平面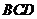 ,
,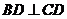 ,若
,若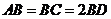 ,求二面角
,求二面角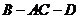 的正弦值
的正弦值
分析:要求二面角的正弦值,首先要找到二面角的平面角
解:过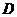 作
作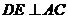 于
于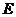 ,过
,过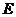 作
作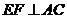 交
交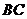 于
于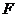 ,连结
,连结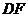 ,
,
则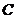 垂直于平面
垂直于平面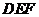 ,
,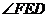 为二面角
为二面角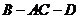 的平面角,
的平面角,
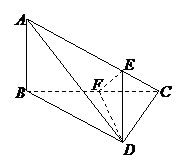 ∴
∴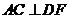 ,
,
又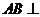 平面
平面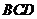 ,
,
∴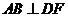 ,
,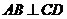 ,
,
∴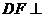 平面
平面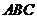 ,
,
∴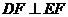 ,
,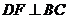 ,
,
又∵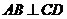 ,
,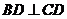 ,
,
∴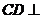 平面
平面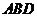 ,∴
,∴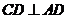 ,
,
设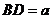 ,则
,则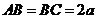 ,
,
在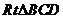 中,
中,
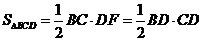 ,∴
,∴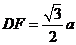 ,
,
同理,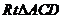 中,
中,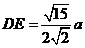 , ∴
, ∴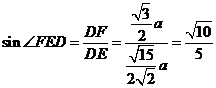 ,
,
所以,二面角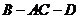 的正弦值为
的正弦值为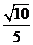 .
.
1  二面角的概念:平面内的一条直线把平面分为两个部分,其中的每一部分叫做半平面;从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面
二面角的概念:平面内的一条直线把平面分为两个部分,其中的每一部分叫做半平面;从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面 若棱为
若棱为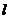 ,两个面分别为
,两个面分别为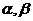 的二面角记为
的二面角记为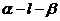 ;二面角的图形表示:
;二面角的图形表示:
第一种是卧式法,也称为平卧式:
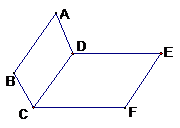
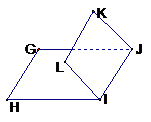
第二种是立式法,也称为直立式:
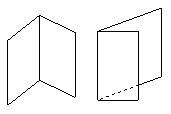
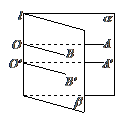
2.二面角的平面角:
(1)过二面角的棱上的一点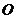 分别在两个半平面内作棱的两条垂线
分别在两个半平面内作棱的两条垂线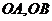 ,则
,则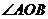 叫做二面角
叫做二面角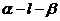 的平面角
的平面角
(2)一个平面垂直于二面角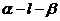 的棱
的棱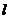 ,且与两半平面交线分别为
,且与两半平面交线分别为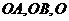 为垂足,则
为垂足,则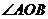 也是
也是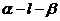 的平面角
的平面角
说明:(1)二面角的平面角范围是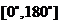 ;
;
(2)二面角的平面角为直角时,则称为直二面角,组成直二面角的两个平面互相垂直
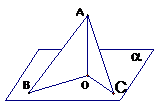
4.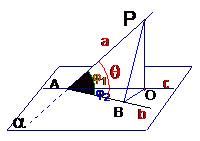 公式:已知平面a的斜线a与a内一直线b相交成θ角,且a与a相交成j1角,a在a上的射影c与b相交成j2角,则有
公式:已知平面a的斜线a与a内一直线b相交成θ角,且a与a相交成j1角,a在a上的射影c与b相交成j2角,则有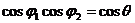 .
.
3.直线和平面所成角
(1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角
一直线垂直于平面,所成的角是直角
一直线平行于平面或在平面内,所成角为0°角.
直线和平面所成角范围:
[0,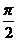 ]
]
(2)定理:斜线和平面所成角是这条斜线和平面内经过斜足的直线所成的一切角中最小的角
1  斜线,垂线,射影
斜线,垂线,射影
 ⑴垂线 自一点向平面引垂线,垂足叫这点在这个平面上的射影. 这个点和垂足间的线段叫做这点到这个平面的垂线段.
⑴垂线 自一点向平面引垂线,垂足叫这点在这个平面上的射影. 这个点和垂足间的线段叫做这点到这个平面的垂线段.
⑵斜线 一条直线和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线 斜线和平面的交点叫斜足;斜线上一点与斜足间的线段叫这点到这个平面的斜线段
斜线和平面的交点叫斜足;斜线上一点与斜足间的线段叫这点到这个平面的斜线段
⑶射影 过斜线上斜足外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面内的射影 垂足和斜足间线段叫这点到这个平面的斜线段在这个平面内的射影
垂足和斜足间线段叫这点到这个平面的斜线段在这个平面内的射影
直线与平面平行,直线在平面由射影是一条直线 直线与平面垂直射影是点
直线与平面垂直射影是点 斜线任一点在平面内的射影一定在斜线的射影上
斜线任一点在平面内的射影一定在斜线的射影上
2.射影长相等定理:从平面外一点向这个平面所引的垂线段和斜线中
 ⑴射影相交两条斜线相交;射影较长的斜线段也较长
⑴射影相交两条斜线相交;射影较长的斜线段也较长
⑵相等的斜线段射影相等,较长的斜线段射影较长
⑶垂线段比任何一条斜线段都短
⑴OB=OCÞAB=AC OB>OCÞAB>AC
⑵AB=ACÞOB=OC AB>ACÞOB>OC
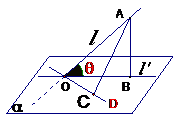 ⑶OA<AB,OA<AC
⑶OA<AB,OA<AC
16、下列各项说法中对原文意思的分析和推断有误的两项是( )
A、现实生活中的霍贝玛穷愁潦倒,但作品里始终有光明和温暖,说明他的灵魂世界是辽远坚韧的,这也是打动作者使作者想要追随他的原因之一。
B、霍贝玛如果知道在他后面还有凡·高这个降生在同一国度的天才也将同他一样穷愁潦倒,他一定不会中断他的风景画创作。
C、霍贝玛这种生前受到否定和排斥,死后较长时间才被接受的遭遇并非绝无仅有,这说明真正伟大的艺术家往往超越他所处的时代。
D、文章多用绚丽的比喻,比如用特征迥异的日、月、星来形容黑屋里的灯,进而比喻霍贝玛的灵魂,既妥帖得体,又抒发了热烈的赞美之情。
E、文章以欣赏霍贝玛的作品为线索,细致深刻的表达了作者对霍贝玛作品的喜爱之情,并由此联想到自己的故乡,说明真正的艺术没有国界。
读读背背
念奴娇 春情
李清照
萧条庭院,又斜风细雨,重门须闭。宠柳娇花寒食近,种种恼人天气。险韵诗成①,扶头酒醒②,别是闲滋味。征鸿过尽,万千心事难寄。
楼上几日春寒,帘垂四面,玉阑干慵倚③。被冷香消新梦觉④,不许愁人不起。清露晨流,新桐初引⑤,多少游春意。日高烟敛,更看今日晴未。
[注释]
①险韵:以生僻字协韵写诗填词。
②扶头酒:能让人精神振作的好酒,饮多则易醉。一说“扶头”为酒名。
③玉阑干:白石栏杆。
④香消:香炉中的香已烧尽。
⑤清露晨流,新桐初引:出自《世说新语·赏誉》。初引:叶初长。
[赏析]这是一首怀人之作。它叙写了寒食节时对丈夫的怀念。开头三句写环境气候,景色萧条。柳、花而用“宠”、“娇”修饰,隐有妒春之意。接着写作诗填词醉酒,但闲愁却无法排解,已有万般怨尤。一句“征鸿过尽,万千心事难寄”,道出词人闲愁的原因:自己思念远行的丈夫,“万千心事”却无法捎寄。下阕开头三句,写出词人懒倚栏杆的愁闷情志,又写出她独宿春闺的种种感觉。“不许愁人不起”,写出作者已失去支撑生活的乐趣。“清露”两句转写新春的可爱,因之产生游春心思。结尾两句最为佳妙:天已放晴,却担心是否真晴,那种心有余悸的感觉,表现得极为凄迷。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com