
13. 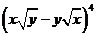 的展开式中
的展开式中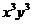 的系数为 6
。
的系数为 6
。
解: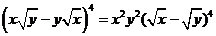 ,只需求
,只需求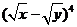 展开式中的含
展开式中的含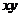 项的系数:
项的系数: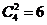


(17)(本小题满分10分)
已知等差数列{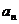 }中,
}中,
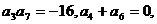 求{
求{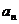 }前n项和
}前n项和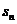 .
. 

解析:本题考查等差数列的基本性质及求和公式运用能力,利用方程的思想可求解。
解:设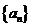 的公差为
的公差为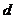 ,则
,则 

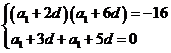
即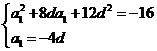
解得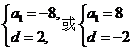
因此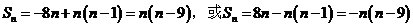
(18)(本小题满分12分)设△ABC的内角A、B、C的对边长分别为a、b、c,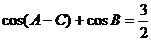 ,
,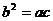 ,求B.
,求B.
解析:本题考查三角函数化简及解三角形的能力,关键是注意角的范围对角的三角函数值的制约,并利用正弦定理得到sinB=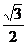 (负值舍掉),从而求出B=
(负值舍掉),从而求出B=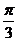 。
。
解:由 cos(A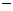 C)+cosB=
C)+cosB=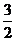 及B=π
及B=π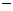 (A+C)得
(A+C)得
cos(A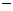 C)
C)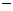 cos(A+C)=
cos(A+C)=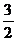 ,
,
cosAcosC+sinAsinC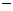 (cosAcosC
(cosAcosC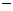 sinAsinC)=
sinAsinC)=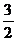 ,
,
sinAsinC=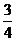 .
.
又由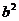 =ac及正弦定理得
=ac及正弦定理得 

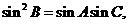
故 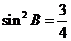 ,
,
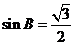 或
或 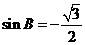 (舍去),
(舍去),
于是 B= 或 B=
或 B=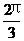 .
.
又由 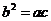 知
知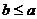 或
或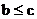
所以 B= 。
。 

(19)(本小题满分12分) 

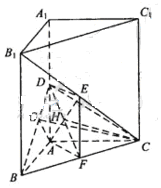
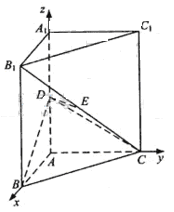
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1
(Ⅰ)证明:AB=AC 

(Ⅱ)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小
解析:本题考查线面垂直证明线面夹角的求法,第一问可取BC中点F,通过证明AF⊥平面BCC1,再证AF为BC的垂直平分线,第二问先作出线面夹角,即证四边形AFED是正方形可证平面DEF⊥平面BDC,从而找到线面夹角求解。此题两问也可建立空间直角坐标系利用向量法求解。
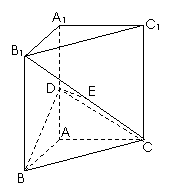 解法一:(Ⅰ)取BC中点F,连接EF,则EF
解法一:(Ⅰ)取BC中点F,连接EF,则EF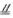
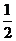
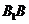 ,从而EF
,从而EF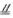 DA。
DA。
连接AF,则ADEF为平行四边形,从而AF//DE。又DE⊥平面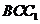 ,故AF⊥平面
,故AF⊥平面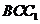 ,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC。
,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC。
(Ⅱ)作AG⊥BD,垂足为G,连接CG。由三垂线定理知CG⊥BD,故∠AGC为二面角A-BD-C的平面角。由题设知,∠AGC=600..
设AC=2,则AG=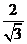 。又AB=2,BC=
。又AB=2,BC=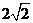 ,故AF=
,故AF=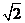 。
。
由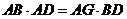 得2AD=
得2AD=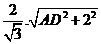 ,解得AD=
,解得AD=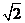 。
。
故AD=AF。又AD⊥AF,所以四边形ADEF为正方形。
因为BC⊥AF,BC⊥AD,AF∩AD=A,故BC⊥平面DEF,因此平面BCD⊥平面DEF。
连接AE、DF,设AE∩DF=H,则EH⊥DF,EH⊥平面BCD。
连接CH,则∠ECH为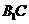 与平面BCD所成的角。
与平面BCD所成的角。 

 因ADEF为正方形,AD=
因ADEF为正方形,AD=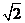 ,故EH=1,又EC=
,故EH=1,又EC=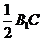 =2,
=2,
所以∠ECH=300,即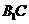 与平面BCD所成的角为300.
与平面BCD所成的角为300.
解法二:
(Ⅰ)以A为坐标原点,射线AB为x轴的正半轴,建立如图所示的直角坐标系A-xyz。
设B(1,0,0),C(0,b,0),D(0,0,c),则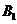 (1,0,2c),E(
(1,0,2c),E(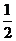 ,
,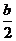 ,c).
,c).
于是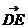 =(
=(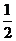 ,
,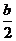 ,0),
,0),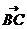 =(-1,b,0).由DE⊥平面
=(-1,b,0).由DE⊥平面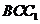 知DE⊥BC,
知DE⊥BC,
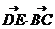 =0,求得b=1,所以 AB=AC。
=0,求得b=1,所以 AB=AC。
(Ⅱ)设平面BCD的法向量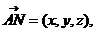 则
则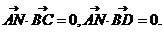
又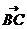 =(-1,1, 0),
=(-1,1, 0),
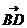 =(-1,0,c),故
=(-1,0,c),故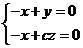


令x=1, 则y=1, z=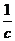 ,
,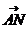 =(1,1,
=(1,1, 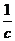 ).
).
又平面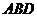 的法向量
的法向量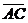 =(0,1,0)
=(0,1,0)
由二面角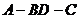 为60°知,
为60°知,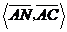 =60°,
=60°,
故 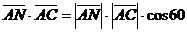 °,求得
°,求得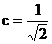


于是 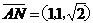 ,
, 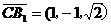
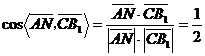 ,
,
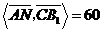 °
°
所以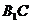 与平面
与平面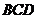 所成的角为30°
所成的角为30°
(20)(本小题满分12分)
某车间甲组有10名工人,其中有4名女工人;乙组有10名工人,其中有6名女工人。现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取4名工人进行技术考核。
(Ⅰ)求从甲、乙两组各抽取的人数;
(Ⅱ)求从甲组抽取的工人中恰有1名女工人的概率;
(Ⅲ)求抽取的4名工人中恰有2名男工人的概率。 

解析:本题考查概率统计知识,要求有正确理解分层抽样的方法及利用分类原理处理事件概率的能力,第一问直接利用分层统计原理即可得人数,第二问注意要用组合公式得出概率,第三问关键是理解清楚题意以及恰有2名男工人的具体含义,从而正确分类求概率。
解:(I)由于甲、乙两组各有10名工人,根据分层抽样原理,要从甲、乙两组中共抽取4名工人进行技术考核,则从每组各抽取2名工人。
(II)记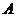 表示事件:从甲组抽取的工人中恰有1名女工人,则
表示事件:从甲组抽取的工人中恰有1名女工人,则
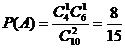


(III)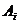 表示事件:从甲组抽取的2名工人中恰有
表示事件:从甲组抽取的2名工人中恰有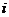 名男工人,
名男工人,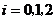
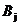 表示事件:从乙组抽取的2名工人中恰有
表示事件:从乙组抽取的2名工人中恰有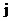 名男工人,
名男工人,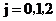
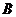 表示事件:抽取的4名工人中恰有2名男工人。
表示事件:抽取的4名工人中恰有2名男工人。
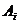 与
与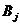 独立,
独立,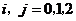 ,且
,且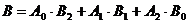
故 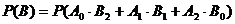
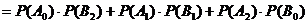
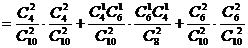
(21)(本小题满分12分)
|
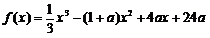
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)若当x≥0时,f(x)>0恒成立,求a的取值范围。 

解析:本题考查导数与函数的综合运用能力,涉及利用导数讨论函数的单调性,第一问关键是通过分析导函数,从而确定函数的单调性,第二问是利用导数及函数的最值,由恒成立条件得出不等式条件从而求出的范围。
解: (I)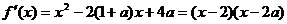


由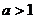 知,当
知,当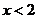 时,
时,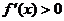 ,故
,故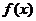 在区间
在区间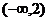 是增函数;
是增函数;
当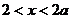 时,
时,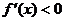 ,故
,故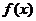 在区间
在区间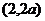 是减函数;
是减函数;
当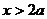 时,
时,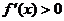 ,故
,故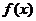 在区间
在区间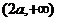 是增函数。
是增函数。
综上,当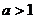 时,
时,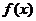 在区间
在区间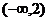 和
和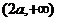 是增函数,在区间
是增函数,在区间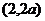 是减函数。
是减函数。
(II)由(I)知,当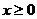 时,
时,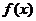 在
在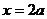 或
或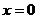 处取得最小值。
处取得最小值。
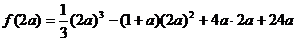
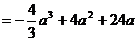
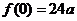
由假设知 

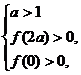 即
即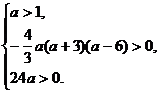 解得 1<a<6
解得 1<a<6
故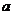 的取值范围是(1,6)
的取值范围是(1,6)
(22)(本小题满分12分)
|
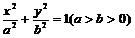
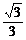
|
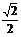
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有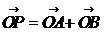 成立?
成立?
若存在,求出所有的P的坐标与l的方程;若不存在,说明理由。
解析:本题考查解析几何与平面向量知识综合运用能力,第一问直接运用点到直线的距离公式以及椭圆有关关系式计算,第二问利用向量坐标关系及方程的思想,借助根与系数关系解决问题,注意特殊情况的处理。
解:(Ⅰ)设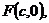 当
当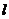 的斜率为1时,其方程为
的斜率为1时,其方程为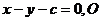 到
到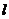 的距离为
的距离为
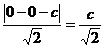
故 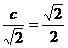 ,
, 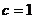


由
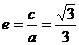
得
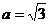 ,
,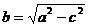 =
=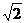
(Ⅱ)C上存在点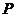 ,使得当
,使得当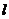 绕
绕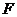 转到某一位置时,有
转到某一位置时,有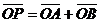 成立。
成立。
由 (Ⅰ)知C的方程为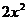 +
+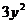 =6. 设
=6. 设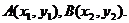
(ⅰ) 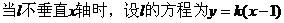
C 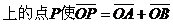 成立的充要条件是
成立的充要条件是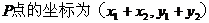 , 且
, 且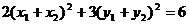
整理得 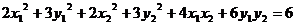
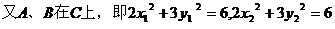
故 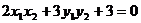 ①
①
将 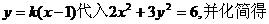
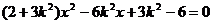


于是 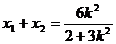 ,
, 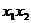 =
=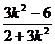 ,
,
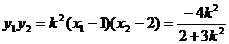
代入①解得,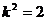 ,此时
,此时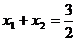
于是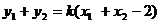 =
=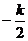 , 即
, 即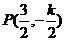


因此, 当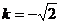 时,
时,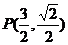 ,
, 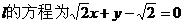 ;
;
当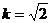 时,
时,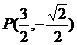 ,
, 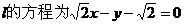 。
。
(ⅱ)当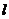 垂直于
垂直于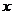 轴时,由
轴时,由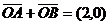 知,C上不存在点P使
知,C上不存在点P使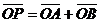 成立。
成立。
综上,C上存在点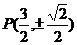 使
使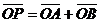 成立,此时
成立,此时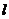 的方程为
的方程为
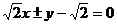


(13)设等比数列{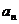 }的前n项和为
}的前n项和为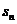 。若
。若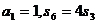 ,则
,则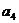 =
×
=
×
答案:3
解析:本题考查等比数列的性质及求和运算,由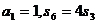 得q3=3故a4=a1q3=3。
得q3=3故a4=a1q3=3。
(14)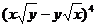 的展开式中
的展开式中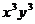 的系数为 ×
的系数为 × 

答案:6
解析:本题考查二项展开式,直接用公式展开,注意根式的化简。
(15)已知圆O: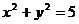 和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于 ×
和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于 ×
答案: 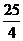
解析:由题意可直接求出切线方程为y-2=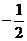 (x-1),即x+2y-5=0,从而求出在两坐标轴上的截距分别是5和
(x-1),即x+2y-5=0,从而求出在两坐标轴上的截距分别是5和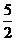 ,所以所求面积为
,所以所求面积为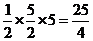 。
。
(16)设OA是球O的半径,M是OA的中点,过M且与OA成45°角的平面截球O的表面得到圆C。若圆C的面积等于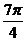 ,则球O的表面积等于 ×
,则球O的表面积等于 ×
答案:8π
解析:本题考查立体几何球面知识,注意结合平面几何知识进行运算,由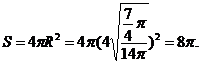
(1)已知全集U={1,2,3,4,5,6,7,8},M ={1,3,5,7},N ={5,6,7},则Cu( M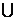 N)=
N)=
(A) {5,7} (B) {2,4} (C){2.4.8} (D){1,3,5,6,7}
答案:C
解析:本题考查集合运算能力。
(2)函数y=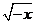 (x
(x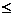 0)的反函数是
0)的反函数是
(A)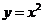 (x
(x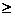 0)
(B)
0)
(B)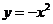 (x
(x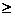 0)
0)
(B)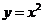 (x
(x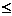 0)
(D)
0)
(D)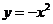 (x
(x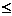 0)
0)
答案:B
解析:本题考查反函数概念及求法,由原函数x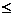 0可知AC错,原函数y
0可知AC错,原函数y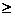 0可知D错,选B.
0可知D错,选B.
(3) 函数y=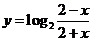 的图像
的图像
(A) 关于原点对称
(B)关于主线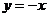 对称
对称
(C) 关于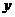 轴对称
(D)关于直线
轴对称
(D)关于直线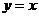 对称
对称
答案:A
解析:本题考查对数函数及对称知识,由于定义域为(-2,2)关于原点对称,又f(-x)=-f(x),故函数为奇函数,图像关于原点对称,选A。
(4)已知△ABC中,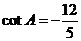 ,则
,则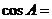
(A) 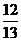 (B)
(B)
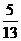 (C)
(C)
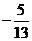 (D)
(D) 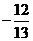
答案:D
解析:本题考查同角三角函数关系应用能力,先由cotA=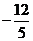 知A为钝角,cosA<0排除A和B,再由
知A为钝角,cosA<0排除A和B,再由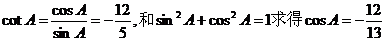 选D
选D
(5) 已知正四棱柱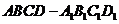 中,
中,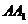 =
=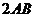 ,
,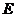 为
为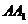 重点,则异面直线
重点,则异面直线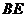
与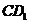 所形成角的余弦值为
所形成角的余弦值为
(A)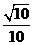 (B)
(B) 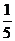 (C)
(C)
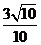 (D)
(D) 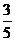


答案:C
解析:本题考查异面直线夹角求法,方法一:利用平移,CD’∥BA' ,因此求△EBA'中∠A'BE即可,易知EB=
,因此求△EBA'中∠A'BE即可,易知EB=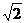 ,A'E=1,A'B=
,A'E=1,A'B=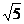 ,故由余弦定理求cos∠A'BE=
,故由余弦定理求cos∠A'BE=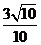 ,或由向量法可求。
,或由向量法可求。
(6) 已知向量a = (2,1), a·b = 10,︱a + b ︱= 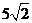 ,则︱b ︱=
,则︱b ︱=
(A)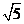 (B)
(B)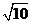 (C)5 (D)25
(C)5 (D)25
答案:C
解析:本题考查平面向量数量积运算和性质,由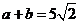 知(a+b)2=a2+b2+2ab=50,得|b|=5 选C。
知(a+b)2=a2+b2+2ab=50,得|b|=5 选C。
(7)设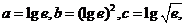 则
则
(A)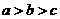 (B)
(B)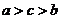 (C)
(C)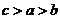 (D)
(D)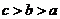
答案:B
解析:本题考查对数函数的增减性,由1>lge>0,知a>b,又c=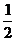 lge, 作商比较知c>b,选B。
lge, 作商比较知c>b,选B。
(8)双曲线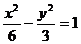 的渐近线与圆
的渐近线与圆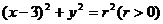 相切,则r=
相切,则r=
(A)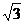 (B)2 (C)3 (D)6
(B)2 (C)3 (D)6
答案:A
解析:本题考查双曲线性质及圆的切线知识,由圆心到渐近线的距离等于r,可求r=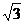
(9)若将函数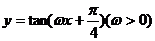 的图像向右平移
的图像向右平移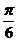 个单位长度后,与函数
个单位长度后,与函数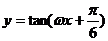 的图像重合,则
的图像重合,则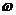 的最小值为
的最小值为
(A)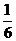 (B)
(B)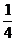 (C)
(C)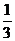 (D)
(D)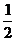


答案:D
解析:本题考查正切函数图像及图像平移,由平移及周期性得出ωmin=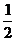
(10)甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中恰有1门相同的选法有
(A)6种 (B)12种 (C)24种 (D)30种
答案:C
解析:本题考查分类与分步原理及组合公式的运用,可先求出所有两人各选修2门的种数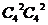 =36,再求出两人所选两门都相同和都不同的种数均为
=36,再求出两人所选两门都相同和都不同的种数均为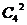 =6,故只恰好有1门相同的选法有24种
。
=6,故只恰好有1门相同的选法有24种
。
(11)已知直线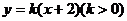 与抛物线C:
与抛物线C: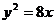 相交A、B两点,F为C的焦点。若
相交A、B两点,F为C的焦点。若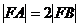 ,则k=
,则k=
(A)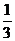 (B)
(B)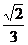 (C)
(C)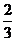 (D)
(D)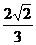
答案:D
解析:本题考查抛物线的第二定义,由直线方程知直线过定点即抛物线焦点(2,0),由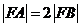 及第二定义知
及第二定义知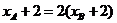 联立方程用根与系数关系可求k=
联立方程用根与系数关系可求k=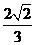 。
。
(12)纸质的正方体的六个面根据其方位分别标记为上、下、东、南、西、北。现在沿该正方体的一些棱将正方体剪开、外面朝上展平,得到右侧的平面图形,则标“△”的面的方位是
(A)南 (B)北 (C)西 (D)下
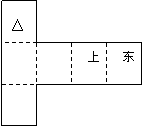


答案:B
解析:.此题用还原立体图方法直接得出结果,使上在正上方依次找到对应面即可。
第Ⅱ卷(非选择题)
本卷共10小题,共90分。
(17)(本小题满分10分)(注意:在试题卷上作答无效)
设等差数列{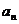 }的前
}的前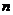 项和为
项和为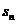 ,公比是正数的等比数列{
,公比是正数的等比数列{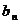 }的前
}的前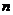 项和为
项和为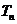 ,
,
已知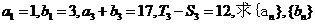 的通项公式.
的通项公式.
[解析]本小题考查等差数列与等比数列的通项公式、前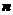 项和,基础题。
项和,基础题。
解:设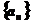 的公差为
的公差为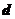 ,数列
,数列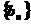 的公比为
的公比为 ,由题得
,由题得
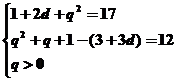 解得
解得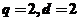
∴ 。
。
(18)(本小题满分12分)(注意:在试用题卷上作答无效)
在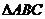 中,内角A、b、c的对边长分别为a、b、c.已知
中,内角A、b、c的对边长分别为a、b、c.已知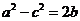 ,且
,且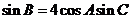 ,求b.
,求b.
[解析]本小题考查正弦定理、余弦定理。
解:由余弦定理得 ,
,
∵ ,
,
∴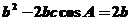 ,即
,即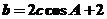 。
。
由正弦定理及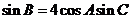 得
得
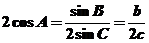 ,
,
∴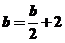 ,即
,即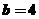 。
。
 (19)(本小题满分12分)(注决:在试题卷上作答无效)
(19)(本小题满分12分)(注决:在试题卷上作答无效)
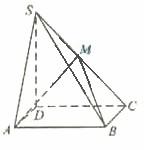
如图,四棱锥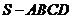 中,底面
中,底面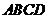 为矩形,
为矩形,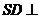 底面
底面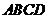 ,
, ,
,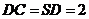 ,点
,点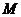 在侧棱
在侧棱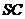 上,
上,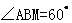 。
。
(I)证明: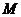 是侧棱
是侧棱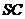 的中点;
的中点;
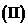 求二面角
求二面角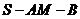 的大小。(同理18)
的大小。(同理18)
[解析]本小题考查空间里的线线关系、二面角,综合题。
(I)解法一:作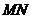 ∥
∥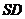 交
交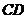 于N,作
于N,作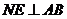 交
交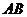 于E,
于E,
 连ME、NB,则
连ME、NB,则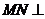 面
面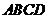 ,
, ,
,
设 ,则
,则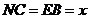 ,
,
在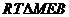 中,
中,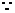
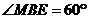
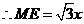 。
。
在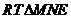 中由
中由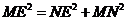
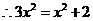
 解得
解得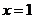 ,从而
,从而
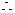 M为侧棱
M为侧棱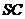 的中点M.
的中点M.
解法二:过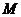 作
作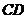 的平行线.
的平行线.
(II)分析一:利用三垂线定理求解。在新教材中弱化了三垂线定理。这两年高考中求二面角也基本上不用三垂线定理的方法求作二面角。
过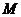 作
作 ∥
∥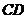 交
交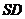 于
于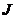 ,作
,作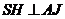 交
交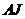 于
于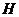 ,作
,作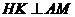 交
交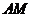 于
于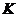 ,则
,则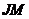 ∥
∥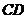 ,
,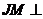 面
面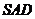 ,面
,面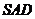
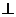 面
面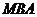 ,
,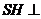 面
面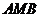
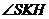 即为所求二面角的补角.
即为所求二面角的补角.
法二:利用二面角的定义。在等边三角形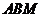 中过点
中过点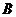 作
作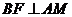 交
交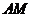 于点
于点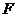 ,则点
,则点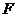 为AM的中点,取SA的中点G,连GF,易证
为AM的中点,取SA的中点G,连GF,易证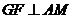 ,则
,则 即为所求二面角.
即为所求二面角.
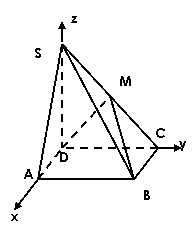 解法二、分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D-xyz,则
解法二、分别以DA、DC、DS为x、y、z轴如图建立空间直角坐标系D-xyz,则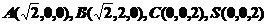 。
。
(Ⅰ)设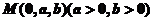 ,则
,则
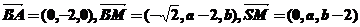 ,
,
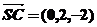 ,由题得
,由题得
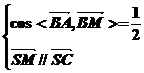 ,即
,即
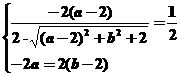 解之个方程组得
解之个方程组得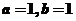 即
即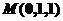
所以 是侧棱
是侧棱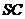 的中点。
的中点。 
法2:设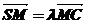 ,则
,则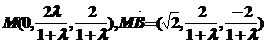
又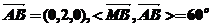
故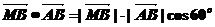 ,即
,即
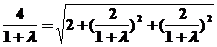 ,解得
,解得 ,
,
所以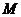 是侧棱
是侧棱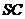 的中点。
的中点。
(Ⅱ)由(Ⅰ)得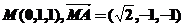 ,又
,又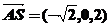 ,
,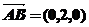 ,
,
设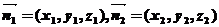 分别是平面
分别是平面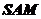 、
、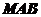 的法向量,则
的法向量,则
 且
且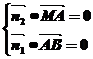 ,即
,即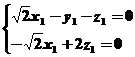 且
且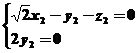
分别令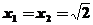 得
得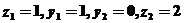 ,即
,即
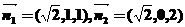 ,
,
∴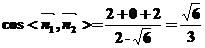

二面角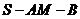 的大小
的大小 。
。
(20)(本小题满分12分)(注意:在试题卷上作答无效)
甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束。假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立。已知前2局中,甲、乙各胜1局。
(Ⅰ)求再赛2局结束这次比赛的概率;
(Ⅱ)求甲获得这次比赛胜利的概率。
[解析]本小题考查互斥事件有一个发生的概率、相互独立事件同时发生的概率,综合题。
解:记“第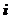 局甲获胜”为事件
局甲获胜”为事件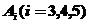 ,“第
,“第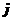 局甲获胜”为事件
局甲获胜”为事件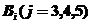 。
。
(Ⅰ)设“再赛2局结束这次比赛”为事件A,则
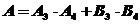 ,由于各局比赛结果相互独立,故
,由于各局比赛结果相互独立,故
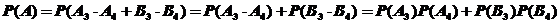
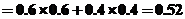 。
。
(Ⅱ)记“甲获得这次比赛胜利”为事件B,因前两局中,甲、乙各胜1局,故甲获得这次比赛胜利当且仅当在后面的比赛中,甲先胜2局,从而
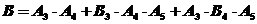 ,由于各局比赛结果相互独立,故
,由于各局比赛结果相互独立,故
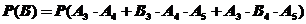
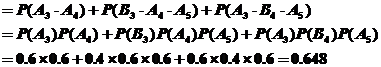
(21)(本小题满分12分)(注意:在试题卷上作答无效) 
已知函数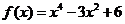 .
.
(Ⅰ)讨论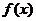 的单调性;
的单调性;
(Ⅱ)设点P在曲线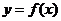 上,若该曲线在点P处的切线
上,若该曲线在点P处的切线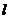 通过坐标原点,求
通过坐标原点,求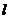 的方程
的方程
[解析]本小题考查导数的应用、函数的单调性,综合题。
解:(Ⅰ)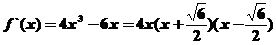
令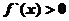 得
得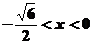 或
或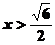 ;
;
令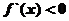 得
得 或
或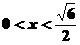
因此,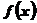 在区间
在区间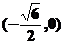 和
和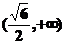 为增函数;在区间
为增函数;在区间 和
和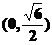 为减函数。
为减函数。
(Ⅱ)设点 ,由
,由 过原点知,
过原点知, 的方程为
的方程为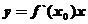 ,
,
因此 ,即
,即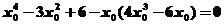 ,整理得
,整理得
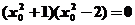 ,解得
,解得 或
或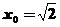 。
。
所以的方程为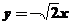 或
或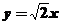

(22)(本小题满分12分)(注意:在试题卷上作答无效)
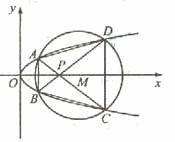 如图,已知抛物线
如图,已知抛物线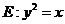
 与圆
与圆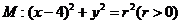 相交于A、B、C、D四个点。
相交于A、B、C、D四个点。
(Ⅰ)求r的取值范围
(Ⅱ)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标。
解:(Ⅰ)将抛物线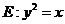 代入圆
代入圆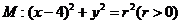 的方程,消去
的方程,消去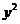 ,整理得
,整理得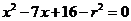 .............(1)
.............(1)
抛物线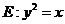 与圆
与圆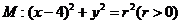 相交于
相交于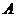 、
、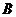 、
、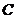 、
、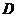 四个点的充要条件是:方程(1)有两个不相等的正根
四个点的充要条件是:方程(1)有两个不相等的正根
∴ 即
即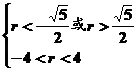 。解这个方程组得
。解这个方程组得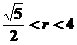
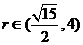 .
.
(II) 设四个交点的坐标分别为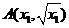 、
、 、
、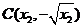 、
、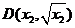 。
。
则由(I)根据韦达定理有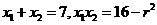 ,
,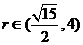
则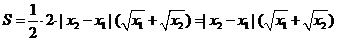
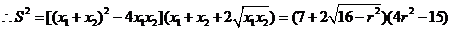
令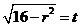 ,则
,则 下面求
下面求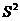 的最大值。
的最大值。
方法1:由三次均值有:
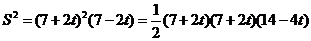
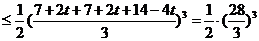
当且仅当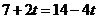 ,即
,即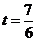 时取最大值。经检验此时
时取最大值。经检验此时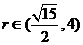 满足题意。
满足题意。
法2:设四个交点的坐标分别为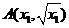 、
、 、
、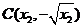 、
、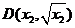
则直线AC、BD的方程分别为
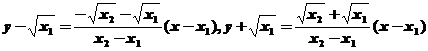
解得点P的坐标为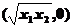 。
。
设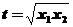 ,由
,由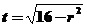 及(Ⅰ)得
及(Ⅰ)得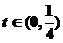

由于四边形ABCD为等腰梯形,因而其面积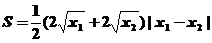
则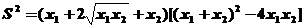 将
将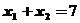 ,
,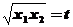 代入上式,并令
代入上式,并令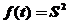 ,等
,等
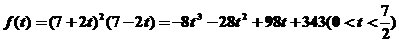 ,
,
∴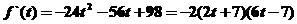 ,
,
令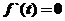 得
得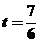 ,或
,或 (舍去)
(舍去)
当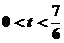 时,
时,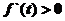 ;当
;当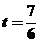 时
时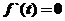 ;当
;当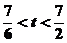 时,
时,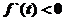
故当且仅当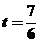 时,
时,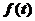 有最大值,即四边形ABCD的面积最大,故所求的点P的坐标为
有最大值,即四边形ABCD的面积最大,故所求的点P的坐标为 。
。
(注意:在试题卷上作答无效)
(13)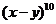 的展开式中,
的展开式中,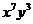 的系数与
的系数与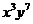 的系数之和等于_____________.
的系数之和等于_____________.
[解析]本小题考查二项展开式通项、基础题。(同理13)
解: 因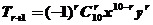 所以有
所以有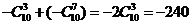 w.w.w.k.s.5.u.c。
w.w.w.k.s.5.u.c。
(14)设等差数列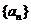 的前
的前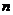 项和为
项和为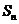 。若
。若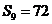 ,则
,则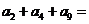 _______________.
_______________.
[解析]本小题考查等差数列的性质、前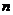 项和,基础题。(同理14)
项和,基础题。(同理14)
解: 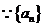 是等差数列,由
是等差数列,由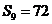 ,得
,得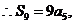

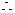
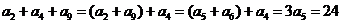 。
。
(15)已知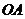 为球
为球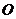 的半径,过
的半径,过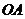 的中点
的中点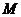 且垂直于
且垂直于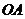 的平面截球面得到圆
的平面截球面得到圆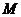 ,若圆
,若圆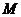 的面积为
的面积为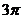 ,则球
,则球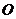 的表面积等于__________________.
的表面积等于__________________.
[解析]本小题考查球的截面圆性质、球的表面积,基础题。
解:设球半径为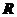 ,圆M的半径为
,圆M的半径为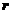 ,则
,则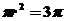 ,即
,即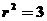 由题得
由题得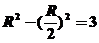 ,所以
,所以 。
。
(16)若直线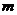 被两平行线
被两平行线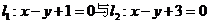 所截得的线段的长为
所截得的线段的长为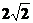 ,则
,则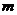 的倾斜角可以是
的倾斜角可以是
①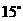 ②
② ③
③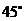 ④
④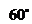 ⑤
⑤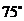

其中正确答案的序号是 .(写出所有正确答案的序号)
[解析]本小题考查直线的斜率、直线的倾斜角、两条平行线间的距离,考查数形结合的思想。
解:两平行线间的距离为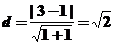 ,由图知直线
,由图知直线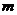 与
与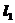 的夹角为
的夹角为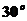 ,
,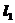 的倾斜角为
的倾斜角为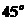 ,所以直线
,所以直线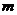 的倾斜角等于
的倾斜角等于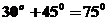 或
或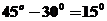 。故填写①或⑤
。故填写①或⑤
3.本卷共10小题,共90分.
(1)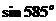 的值为
的值为
(A) 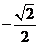 (B)
(B)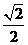 (C)
(C)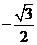 (D)
(D) 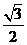
[解析]本小题考查诱导公式、特殊角的三角函数值,基础题。
解: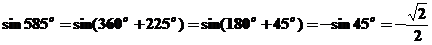 ,故选择A。
,故选择A。
(2)设集合A={4,5,6,7,9},B={3,4,7,8,9},全集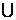 =A
=A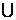 B,则集合[u (A
B,则集合[u (A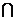 B)中的元素共有
B)中的元素共有
(A) 3个 (B) 4个 (C)5个 (D)6个
[解析]本小题考查集合的运算,基础题。(同理1)
解: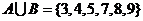 ,
,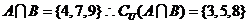 故选A。也可用摩根律:
故选A。也可用摩根律: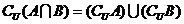
(3)不等式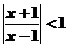 的解集为D
的解集为D 
(A)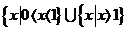 (B)
(B)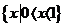
(C) 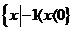 (D)
(D)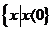
[解析]本小题考查解含有绝对值的不等式,基础题。
解: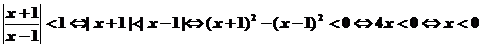 ,
,
故选择D。
(4)已知tan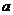 =4,cot
=4,cot =
=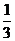 ,则tan(a+
,则tan(a+ )=
)=
(A)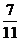 (B)
(B)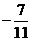 (C)
(C) 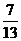 (D)
(D) 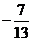
[解析]本小题考查同角三角函数间的关系、正切的和角公式,基础题。
解:由题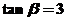 ,
,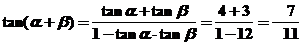 ,故选择B。
,故选择B。
(5)设双曲线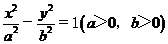 的渐近线与抛物线
的渐近线与抛物线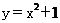 相切,则该双曲线的离心率等于
相切,则该双曲线的离心率等于
(A)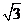 (B)2 (C)
(B)2 (C)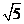 (D)
(D)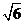
[解析]本小题考查双曲线的渐近线方程、直线与圆锥曲线的位置关系、双曲线的离心率,基础题。
解:由题双曲线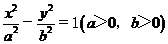 的一条渐近线方程为
的一条渐近线方程为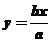 ,代入抛物线方程整理得
,代入抛物线方程整理得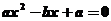 ,因渐近线与抛物线相切,所以
,因渐近线与抛物线相切,所以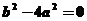 ,即
,即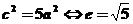 ,故选择C。
,故选择C。
(6)已知函数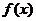 的反函数为
的反函数为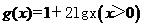 ,则
,则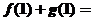
(A)0 (B)1 (C)2 (D)4
[解析]本小题考查反函数,基础题。
解:由题令 得
得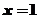 ,即
,即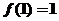 ,又
,又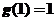 ,所以
,所以 ,故选择C。
,故选择C。
(7)甲组有5名男同学、3名女同学;乙组有6名男同学、2名女同学,若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有
(A)150种 (B)180种 (C)300种 (D)345种
[解析]本小题考查分类计算原理、分步计数原理、组合等问题,基础题。
解:由题共有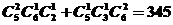 ,故选择D。
,故选择D。
(8)设非零向量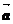 、
、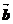 、
、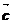 满足
满足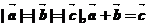 ,则
,则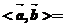
(A)150°B)120° (C)60° (D)30°
[解析]本小题考查向量的几何运算、考查数形结合的思想,基础题。
解:由向量加法的平行四边形法则,知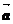 、
、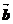 可构成菱形的两条相邻边,且
可构成菱形的两条相邻边,且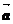 、
、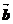 为起点处的对角线长等于菱形的边长,故选择B。
为起点处的对角线长等于菱形的边长,故选择B。
(9)已知三棱柱 的侧棱与底面边长都相等,
的侧棱与底面边长都相等,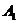 在底面
在底面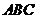 上的射影为
上的射影为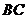 的中点,则异面直线
的中点,则异面直线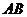 与
与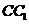 所成的角的余弦值为
所成的角的余弦值为
(A)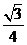 (B)
(B) 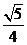 (C)
(C) 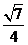 (D)
(D)
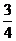
[解析]本小题考查棱柱的性质、异面直线所成的角,基础题。(同理7)
解:设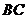 的中点为D,连结
的中点为D,连结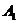 D,AD,易知
D,AD,易知 即为异面直线
即为异面直线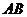 与
与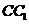 所成的角,由三角余弦定理,易知
所成的角,由三角余弦定理,易知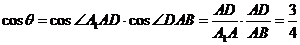 .故选D
.故选D
(10) 如果函数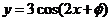 的图像关于点
的图像关于点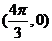 中心对称,那么
中心对称,那么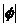 的最小值为
的最小值为
(A)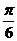 (B)
(B) 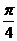 (C)
(C) 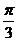 (D)
(D)
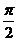
[解析]本小题考查三角函数的图象性质,基础题。
解: 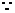 函数
函数 的图像关于点
的图像关于点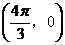 中心对称
中心对称
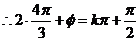
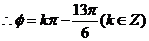 由此易得
由此易得 .故选A
.故选A
(11)已知二面角 为600 ,动点P、Q分别在面
为600 ,动点P、Q分别在面 内,P到
内,P到 的距离为
的距离为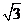 ,Q到
,Q到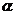 的距离为
的距离为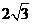 ,则P、Q两点之间距离的最小值为
,则P、Q两点之间距离的最小值为
[解析]本小题考查二面角、空间里的距离、最值问题,综合题。(同理10)
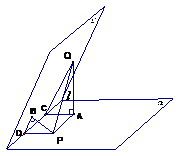 解:如图分别作
解:如图分别作
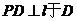 ,连
,连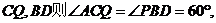

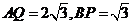 ,
,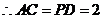
又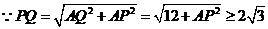
当且仅当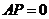 ,即
,即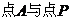 重合时取最小值。故答案选C。
重合时取最小值。故答案选C。
(12)已知椭圆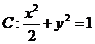 的右焦点为F,右准线
的右焦点为F,右准线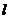 ,点
,点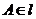 ,线段AF交C于点B。若
,线段AF交C于点B。若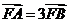 ,则
,则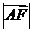 =
=
(A) 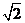 (B) 2 (C)
(B) 2 (C) 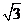 (D) 3
(D) 3
[解析]本小题考查椭圆的准线、向量的运用、椭圆的定义,基础题。
解:过点B作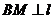 于M,并设右准线
于M,并设右准线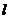 与x轴的交点为N,易知FN=1.由题意
与x轴的交点为N,易知FN=1.由题意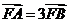 ,故
,故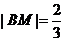 .又由椭圆的第二定义,得
.又由椭圆的第二定义,得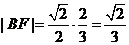
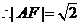 .故选A
.故选A
2009年普通高等学校招生全国统一考试
文科数学(必修 选修Ⅰ)
选修Ⅰ)
第Ⅱ卷
2.第Ⅱ卷共7页,请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答,在试题卷上作答无效.
3、面面成角(二面角)
方法一:直接作二面角(需要证明)
方法二:面积法(一定有垂直才能用)
PC ┴ 面ABC,记二面角P-AB-C为θ,则
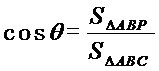
(先写公共边/点,再按垂线依次往后写,垂足放在分子)
附:使用时,可能会正弦定理与余弦定理搭配使用。
正弦定理: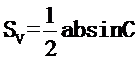
余弦定理: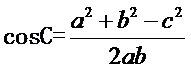
方法三:向量法
求,β所成二面角x,先求α ,法向量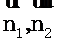 所成的角θ
所成的角θ
则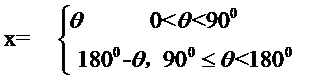
求距离
点到平面的距离
方法一:等体积法(注意点的平移,以及体积的等量代换)
例:求点B到PAC的距离h(已知PB┴面ABC)
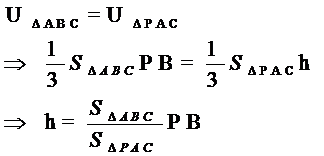
(注意余弦定理,正弦定理的综合应用)
方法二:向量法
同上,设面PAC的法向量为n (可以自行求出),在面PAC上任取一点,不妨碍取P,则
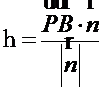
 P
P
A B C
2、线线成角
几何法:平移(中点平移,顶点平移)
向量法:
a ,b 夹角,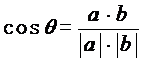
(几何法时常用到余弦定理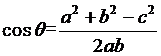 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com