4．已知点P(1,4)在圆C：x²+y²+2ax－4y+b＝0上，点P关于直线x+y－3＝0的对称点也在圆C上，则a＝________，b＝________.

解析：点P(1,4)在圆C：x²+y²+2ax－4y+b＝0上，所以2a+b+1＝0，点P关于直线x+y－3＝0的对称点也在圆C上，所以圆心　 (－a,2)在直线x+y－3＝0上，即－a+2－3＝0，解得a＝－1，b＝1.

3．(2009年高考上海卷改编)点P(4，－2)与圆x²+y²＝4上任一点连线的中点轨迹方程是________________．

解析：设圆上任一点坐标为(x₀，y₀)，则x₀²+y₀²＝4，连线中点坐标为(x，y)，

则⇒代入x₀²+y₀²＝4中得(x－2)²+(y+1)²＝1.

2．(2010年扬州调研)若直线ax+by＝1过点A(b，a)，则以坐标原点O为圆心，OA长为半径的圆的面积的最小值是___．

解析：∵直线ax+by＝1过点A(b，a)，∴ab+ab＝1，∴ab＝，又OA＝，∴以O为圆心，OA长为半径的圆的面积：S＝π·OA²＝(a²+b²)π≥2ab·π＝π，∴面积的最小值为π.

1．(2010年福州质检)圆心在直线2x－3y－1＝0上的圆与x轴交于A(1,0)，B(3,0)两点，则圆的方程为________________．

解析：所求圆与x轴交于A(1,0)，B(3,0)两点，故线段AB的垂直平分线x＝2过所求圆的圆心，又所求圆的圆心在直线2x－3y－1＝0上，所以两直线的交点坐标即为所求圆的圆心坐标，解之得圆心坐标为(2,1)，进一步可求得半径为，所以圆的标准方程为(x－2)²+(y－1)²＝2.

6．已知点A(－3,0)，B(3,0)，动点P满足|PA|＝2|PB|.

(1)若点P的轨迹为曲线C，求此曲线的方程；

(2)若点Q在直线l：x+y+3＝0上，直线l₂经过点Q且与曲线C只有一个公共点M，求|QM|的最小值，并求此时直线l₂的方程．

解：(1)设点P的坐标为(x，y)，

则＝2，

化简可得(x－5)²+y²＝16即为所求．

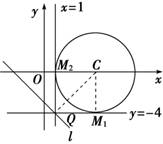
(2)曲线C是以点(5,0)为圆心，4为半径的圆，如图则直线l₂是此圆的切线，连结CQ，则|QM|＝＝，

当CQ⊥l₁时，|CQ|取最小值，|CQ|＝＝4，

此时|QM|的最小值为＝4，这样的直线l₂有两条，设满足条件的两个公共点为M₁，M₂，

易证四边形M₁CM₂Q是正方形，∴l₂的方程是x＝1或y＝－4.

B组

5．(原创题)圆x²+y²－4x+2y+c＝0与y轴交于A、B两点，其圆心为P，若∠APB＝90°，则实数c的值是________．

解析：当∠APB＝90°时，只需保证圆心到y轴的距离等于半径的倍．由于圆的标准方程为(x－2)²+(y+1)²＝5－c，即2＝×，解得c＝－3.

4．(2009年高考宁夏、海南卷改编)已知圆C₁：(x+1)²+(y－1)²＝1，圆C₂与圆C₁关于直线x－y－1＝0对称，则圆C₂的方程为________________．

解析：圆C₁：(x+1)²+(y－1)²＝1的圆心为(－1,1)．圆C₂的圆心设为(a，b)，C₁与C₂关于直线x－y－1＝0对称，∴解得圆C₂的半径为1，∴圆C₂的方程为(x－2)²+(y+2)²＝1.

3．(2010年广东汕头调研)已知D是由不等式组，所确定的平面区域，则圆x²+y²＝4在区域D内的弧长为________．

答案：π

2．若圆C的半径为1，圆心在第一象限，且与直线4x－3y＝0和x轴都相切，则该圆的标准方程是________．

解析：由题意，设圆心(x_0,1)，∴＝1，解得x₀＝2或x₀＝－(舍)，

∴所求圆的方程为(x－2)²+(y－1)²＝1.

1．若圆x²+y²－2kx+2y+2＝0(k>0)与两坐标轴无公共点，那么实数k的取值范围为________．

解析：圆的方程为(x－k)²+(y+1)²＝k²－1，圆心坐标为(k，－1)，半径r＝，若圆与两坐标无公共点，即，解得1<k<.