
20.(本小题满分10分)已知数列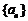 中,
中,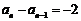 ,
,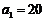 .
.
(1)求数列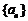 的通项公式
的通项公式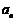 及前
及前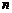 项和
项和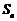 ;(2)求使
;(2)求使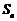 最大的序号
最大的序号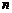 的值.
的值.
(3)求数列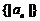 的前
的前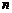 项和
项和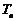 .
.
[解析](1)数列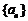 为等差数列,公差
为等差数列,公差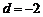 ,
,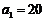
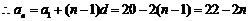 .
.
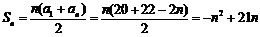 .
.
(2)令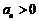 得
得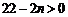 ,
,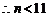 , 令
, 令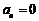 得
得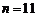 .
.
故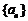 中前10项为正,第11项为零,从第12项开始为负,故使
中前10项为正,第11项为零,从第12项开始为负,故使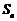 最大的
最大的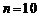 或
或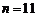 .
.
(3)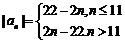
当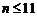 时,
时,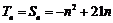 ;
;
当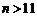 时,
时,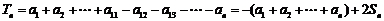
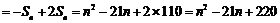
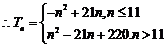
19.(本小题满分8分)已知直线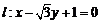 ,一个圆的圆心
,一个圆的圆心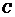 在
在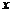 轴正半轴上,且该圆与直线
轴正半轴上,且该圆与直线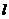 和
和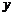 轴均相切.
轴均相切.
(1)求该圆的方程;
(2)直线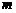 :
: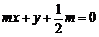 与圆
与圆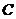 交于
交于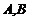 两点,且
两点,且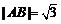 ,求
,求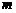 的值.
的值.
[解析](1)设圆心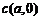 ,
,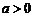 ,半径为
,半径为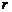 ,则
,则
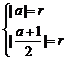
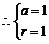
所求圆的方程为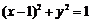 .
.
(2)作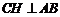 垂足为
垂足为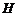 ,则
,则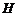 为
为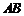 中点
中点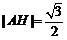 ,
,
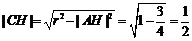 ,即点
,即点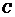 到直线
到直线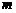 的距离为
的距离为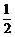 .
.
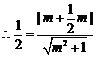
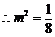 ,
,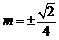 .
.
18.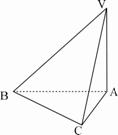 (本小题满分8分)如图,已知三棱锥
(本小题满分8分)如图,已知三棱锥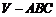 中,
中,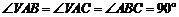 且
且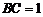 ,
,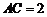 ,
,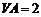 .
.
(1)求证: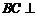 平面
平面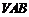 .
.
(2)求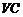 与平面
与平面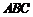 所成的角.
所成的角.
(3)求二面角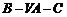 的平面角.
的平面角.
[解析](1)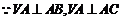 ,
,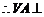 平面
平面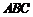
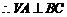 又
又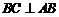
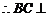 平面
平面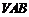 .
.
(2)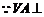 平面
平面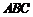
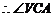 为
为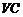 与平面
与平面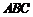 所成的角
所成的角
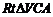 中,
中,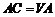
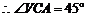
即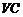 与平面
与平面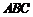 所成的角为
所成的角为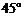 .
.
(3)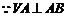 ,
,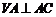
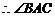 为
为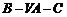 的平面角.
的平面角.
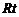
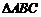 中,
中,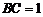 ,
,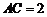
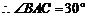
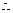 二面角
二面角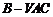 的平面角为
的平面角为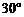 .
.
17.(本小题满分8分)已知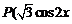 ,
,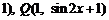 .函数
.函数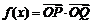 .(
.(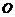 为坐标原点)
为坐标原点)
(Ⅰ)求函数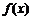 的解析式; (Ⅱ)求函数
的解析式; (Ⅱ)求函数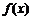 的最小正周期及最值;
的最小正周期及最值;
(Ⅲ)该函数图像可由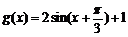 的图像经过怎样的变换得来?
的图像经过怎样的变换得来?
[解析](Ⅰ)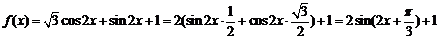
(Ⅱ)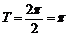 ,
,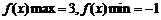 .
.
(Ⅲ)由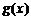 图象上每点横坐标缩短到原来的
图象上每点横坐标缩短到原来的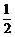 ,而纵坐标不变.
,而纵坐标不变.
16.(本小题满分6分)已知甲、乙两名篮球运动员每场比赛得分的原始记录用如下茎叶图表示:
|
甲 |
|
乙 |
|
8 4 6 3 3 6 8 3 8 9 1 |
0 1 2 3 4 5 |
2 5 5 4 1 6 1 6 7 9 4 9 5 0 |
(1)按从小到大的顺序写出甲运动员的得分;
(2)求甲、乙运动员得分的中位数;
(3)估计乙运动员在一场比赛中得分落在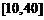 内的概率.
内的概率.
[解析](1)甲运动员得分为:8,13,14,16,23,26,28,33,38,39,51.
(2)甲的中位数为26,乙的中位数为36.
(3)设乙运动员得分在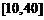 为事件A,则
为事件A,则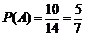 .
.
15.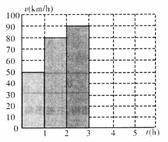 一辆汽车在某段路程中的行驶速度
一辆汽车在某段路程中的行驶速度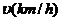 与时间
与时间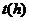 的关系如右图.假设这辆汽车的里程表在汽车行驶前的读数为2009km,则汽车行驶这段路程时汽车里程表读数
的关系如右图.假设这辆汽车的里程表在汽车行驶前的读数为2009km,则汽车行驶这段路程时汽车里程表读数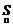 与时间
与时间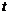 的解析式为:
的解析式为:
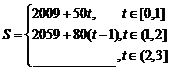 .
.
[答案]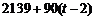
14.用20cm长的铁丝分成两段,每段各折成一个等边三角形,则这两个等边三角形面积和的最大值为 cm2.
[答案]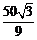
13.等比数列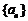 中,
中,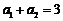 ,
,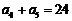 ,则数列
,则数列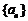 的通项公式
的通项公式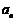 = .
= .
[答案]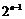
12.已知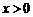 ,当
,当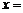 时,
时,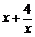 的最小值为4.
的最小值为4.
[答案]2
11.已知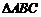 中,
中,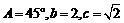 ,则
,则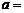 .
.
[答案]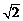
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com