
2.会用平均值定理求最大或最小值;
1.掌握两个正数的算术平均数不小于几何平均数的定理;
12. 证明:过抛物线y=a(x-x1)·(x-x2)(a≠0,x1<x2)上两点A(x1,0)、B(x2,0)的切线,与x轴所成的锐角相等.
解:y′=2ax-a(x1+x2),
y′|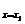 =a(x1-x2),即kA=a(x1-x2),y′|
=a(x1-x2),即kA=a(x1-x2),y′|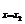 =a(x2-x1),即kB=a(x2-x1).
=a(x2-x1),即kB=a(x2-x1).
设两条切线与x轴所成的锐角为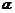 、β,则tan
、β,则tan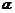 =|kA|=|a(x1-x2)|,
=|kA|=|a(x1-x2)|,
tanβ=|kB|=|a(x2-x1)|,故tan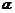 =tanβ.
=tanβ.
又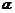 、β是锐角,则
、β是锐角,则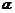 =β.
=β.
11.(2005福建) 已知函数
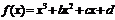 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为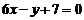 .
.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
解:(Ⅰ)由f(x)的图象经过P(0,2),知d=2,
所以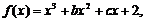
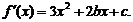
由在M(-1,f(-1))处的切线方程是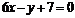 ,知
,知
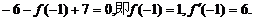
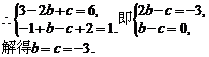
故所求的解析式是 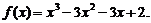
(Ⅱ)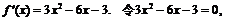
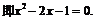
解得 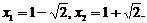
当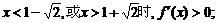
当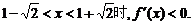
故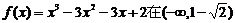 内是增函数,在
内是增函数,在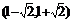 内是减函数,在
内是减函数,在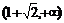 内是增函数.
内是增函数.
考查知识:函数的单调性、导数的应用等知识,考查运用数学知识分析问题和解决问题的能力.
10. 如果曲线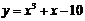 的某一切线与直线
的某一切线与直线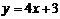 平行,求切点坐标与切线方程.
平行,求切点坐标与切线方程.
解: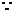 切线与直线
切线与直线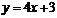 平行, 斜率为4
平行, 斜率为4
又切线在点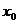 的斜率为
的斜率为
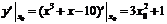
∵ 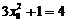 ∴
∴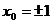
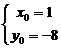 或
或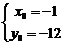
∴切点为(1,-8)或(-1,-12)
切线方程为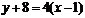 或
或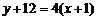
即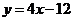 或
或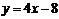
9.下列函数的导数
①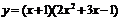
②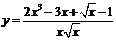
③f(x)=e-x(cosx+sinx)
分析:利用导数的四则运算求导数
①法一: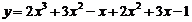
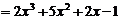
∴ 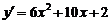
法二:
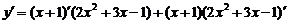 =
=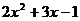 +
+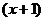
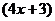
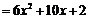
② 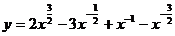
∴ 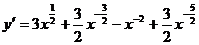
③f/(x)=-e-x(cosx+sinx)+e-x(-sinx+cosx)
=-2e-xsinx,
8.由消y得:(x-2)(x2+4x+8)=0,∴x=2
∵y′=(2-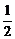 x2)′=-x,∴y′|x=2=-2
x2)′=-x,∴y′|x=2=-2
又y′=(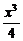 -2)′=
-2)′=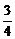 x2,∴当x=2时,y′=3
x2,∴当x=2时,y′=3
∴两曲线在交点处的切线斜率分别为-2、3,
|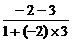 |=1 ∴夹角为
|=1 ∴夹角为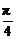
[解答题]
6.y=4x-4;7.∵f(1)=0,
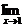
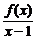 =2,
=2,
∴f′(1)=
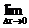
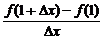 =
=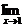
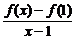 =
=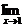
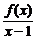 =2
=2
8.曲线y=2-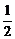 x2与y=
x2与y=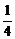 x3-2在交点处的切线夹角是__________(以弧度数作答)
x3-2在交点处的切线夹角是__________(以弧度数作答)
简答.提示:1-4.BADA;5. 1,2,4秒末;
7. 设f(x)在x=1处连续,且f(1)=0,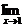
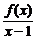 =2,则f′(1)=_______
=2,则f′(1)=_______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com