
4.知识产权在技术领域的重要作用:a
知识产权是人们基于自己的智力活动创造的成果和经营活动的标记、信誉而依法享有的权利。狭义的知识产权包括著作权、专利权、商标权三部分。专利在产权保护制度下对技术活动的重要性知识产权制度允许专利所有权人对专利技术具有一定的性,使其专利技术和产品在一定时间内独占市场,从而得到丰厚的回报,保持发明创造的积极性,使技术创新活动趋向良性循环专利的特性:独占性、时间性、地域性
专利申请步骤:提交申请阶段→受理阶段→初审阶段→公布阶段→实审阶段→授权阶段
3.技术与科学的区别与联系:b
技术与科学的区别与联系
|
科学是对各种事实和现象进行观察、分类、归纳、演绎、分析、推理、计算和实验,从而发现规律,并予以验证和公式化的知识体系 |
技术则是人类为了满足自身的需要和愿望对大自然进行的改造 |
||
|
科学侧重认识自然,力求有所发现 |
技术侧重利用和合理地改造自然,力求有所发明 |
||
|
科学回答“是什么”“为什么”的问题 |
技术则更多地回答“怎么办”的问题 |
||
|
科学通过实验验证假设,形成结论 |
技术则通过试验,验证方案的可行性与合理性,并实现优化 |
||
科学促进了技术的发展,技术推动了科学的进步。
2.技术的两面性:a任何事物客观上都有两面性,技术也不例外。它既可以给人们带来福音,也可能给人们带来危害。(例:电池可以带来光明和动力,也可以带来严重的环境污染。网络技术 方便人们交流沟通,但也有人利用网络犯罪。B超技术 可以用于医疗,但也有人进行胎儿鉴别 )
1. 技术的发展与发明和革新关系:b
技术的基本特性:目的性、创新性、综合性、两面性、专利性。创新是技术发展的核心。每一项技术的问世都是创新的结果。技术的发展需要创新,技术创新表现为技术革新和技术发明。技术创新是一个艰难而曲折的历程。(例:瓦特蒸汽机与第一次技术革命。显示器的革新和电视机的创新,阴极射线管(CRT))
3、技术对自然的价值:c(1)依靠技术,人类得以利用自然和改造,并与自然保持和谐共处的友好关系。(例都江堰)(2)人类利用技术开发、改造自然时,应把握合理的尺度,要注意对自然的保护,不能忽视技术或产品对环境可能造成的负面影响。(3)技术的发展给自然环境带来了问题,但也给解决这些问题提供了可能(例:物料的再循环工艺)
2、技术对生活、生产、文化等方面的影响:a
技术促进社会的发展。技术丰富社会文化内容。技术改变社会生活方式。是推动社会发展和文明进步的主要动力之一。具体为:⑴ 技术是社会财富积累的一种形式,对社会生产具有直接的经济意义。
⑵ 随着技术的发展,劳动力结构也发了较大的变化,第一第二产业从业者数量减少,第三产业从业者数量大幅度增加。如因为农业技术的发展与劳作方式的变革使农业从业人口减少。 ⑶ 技术不仅为生产提供了先进的手段和工具,提高了生产效率和经济效益,而且丰富了人们的社会生活,使人们衣、食、住、行、交往、娱乐、教育等方面都发生了改变。 ⑷ 技术进步不仅带动社会生产的发展和社会活动的变化,而且渗透到军事、政治、文化各领域。
1、技术对人类的价值: a
技术是人类为满足自身的需求和愿望对大自然进行的改造。它具有保护人、解放人和发展人的作用[保护人](例:原始人随身拾磨制好的石器,现代人对疟疾、天花、肺结核等疾病不再恐慌)[解放人](例:体力解放:自行车、内燃动力、电力,手机--信息传递)[发展人](例:爱迪生、袁隆平)
9、已知曲线C:xy=1,过C上一点 作一斜率为
作一斜率为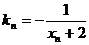 的直线交曲线C于另一点
的直线交曲线C于另一点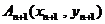 ,点列
,点列 的横坐标构成数列{
的横坐标构成数列{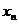 },其中
},其中 .
.
(1)求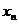 与
与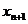 的关系式;
的关系式;
(2)求证:{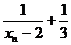 }是等比数列;
}是等比数列;
(3)求证: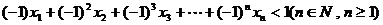 。
。
解:(1)过C: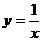 上一点
上一点 作斜率为
作斜率为 的直线交C于另一点
的直线交C于另一点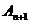 ,
,
则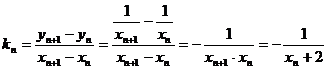 ,
----------------------------3分
,
----------------------------3分
(前三个式子各式1分)
于是有: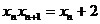 即:
即: ----------------------------4分
----------------------------4分
(2)记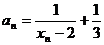 ,则
,则
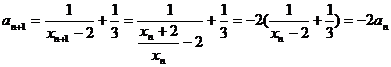 , ----------------6分
, ----------------6分
因为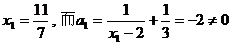 ,
,
因此数列{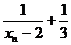 }是等比数列。
----------------------------8分
}是等比数列。
----------------------------8分
(3)由(2)可知: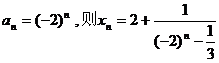 ,
,
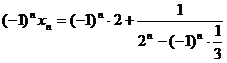 。
----------------------9分
。
----------------------9分
当n为偶数时有:
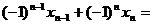
=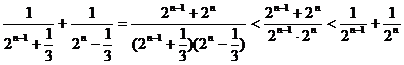 , -------------11分
, -------------11分
于是
①在n为偶数时有:
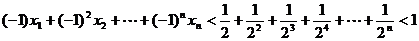 。 ----------12分
。 ----------12分
②在n为奇数时,前n-1项为偶数项,于是有:

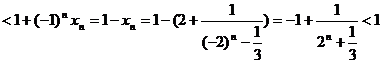 。 -----------------13分
。 -----------------13分
综合①②可知原不等式得证。
8、已知数列 的首项
的首项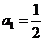 ,前
,前 项和
项和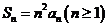 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设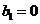 ,
,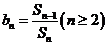 ,
, 为数列
为数列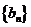 的前
的前 项和,求证:
项和,求证: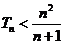 .
.
解:(Ⅰ)由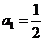 ,
,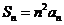 ,
①
,
①
∴
 ,
②
,
②
①-②得: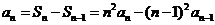 ,即
,即
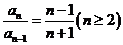 ,
4分
,
4分
∵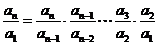
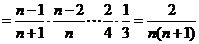 ,
,
∴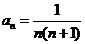 。
8分
。
8分
(Ⅱ)∵ ,∴
,∴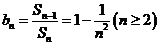 ,
10分
,
10分
∴ 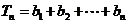


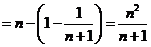 .
.
故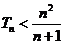 .
14分
.
14分
7、已知数列 是等差数列,
是等差数列, 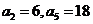 ;数列
;数列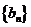 的前n项和是
的前n项和是 ,且
,且 .
.
(Ⅰ) 求数列 的通项公式; (Ⅱ) 求证:数列
的通项公式; (Ⅱ) 求证:数列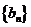 是等比数列;
是等比数列;
(Ⅲ) 记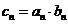 ,求
,求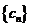 的前n项和
的前n项和
解:(Ⅰ)设 的公差为
的公差为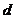 ,则:
,则: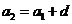 ,
,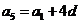 ,
,
∵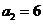 ,
, ,∴
,∴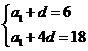 ,∴
,∴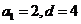 .
.
∴ .
.
(Ⅱ)当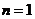 时,
时, ,由
,由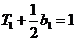 ,得
,得 .
.
当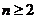 时,
时, ,
,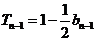 ,
,
∴ ,即
,即 .
.
∴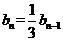 .
.
∴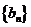 是以
是以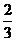 为首项,
为首项,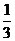 为公比的等比数列.
为公比的等比数列.
(Ⅲ)由(2)可知: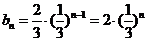 .
.
∴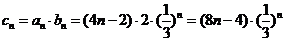 .
.
∴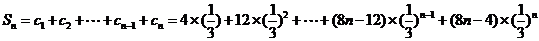 .
.
∴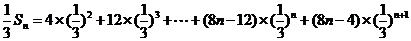 .
.
∴
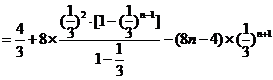
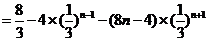 .
.
∴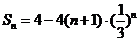 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com