
6.在等比数列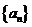 中,
中,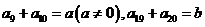 ,则
,则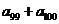 等于 。
等于 。
5.设Sn=是等差数列{an}的前n项和,a12=-8,S9=-9,则S16= .
4.已知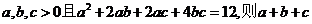 的最小值为
.
的最小值为
.
3.若a是 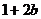 与
与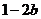 的等比中项,则
的等比中项,则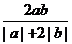 的最大值为
。
的最大值为
。
2.设M是△ABC内一点,且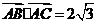 ,∠BAC=30º,定义f(M)=(m,n,p),其中m、n、p分别是△MBC、△MCA、△MAB的面积,若f(M)=(
,∠BAC=30º,定义f(M)=(m,n,p),其中m、n、p分别是△MBC、△MCA、△MAB的面积,若f(M)=(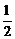 ,x,y),则
,x,y),则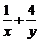 的最小值为
.
的最小值为
.
1. 若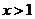 ,则函数
,则函数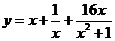 的最小值为 。
的最小值为 。
2.
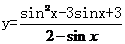
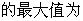 ,
,
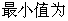 .
.
[例2]设数列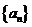 满足
满足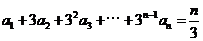 ,
,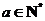 .
.
(Ⅰ)求数列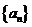 的通项; (Ⅱ)设
的通项; (Ⅱ)设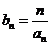 ,求数列
,求数列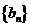 的前
的前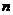 项和
项和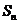 .
.
[变式]已知二次函数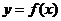 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为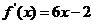 ,数列
,数列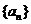 的前n项和为
的前n项和为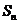 ,点
,点 均在函数
均在函数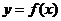 的图像上。(Ⅰ)、求数列
的图像上。(Ⅰ)、求数列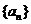 的通项公式;(Ⅱ)、设
的通项公式;(Ⅱ)、设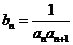 ,
,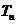 是数列
是数列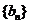 的前n项和,求使得
的前n项和,求使得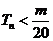 对所有
对所有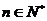 都成立的最小正整数m;
都成立的最小正整数m;
[例3] 已知数列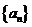 中的相邻两项
中的相邻两项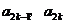 是关于
是关于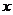 的方程
的方程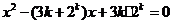 的两个根,且
的两个根,且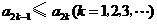 .
.
(I)求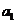 ,
,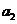 ,
,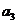 ,
,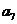 ; (II)求数列
; (II)求数列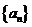 的前
的前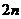 项和
项和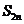 ;
;
(Ⅲ)(理)记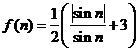 ,
,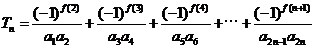 ,
,
求证: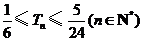 .
.
[能力提升训练]
7.倒序相加法求和
[突 破 重 难 点]
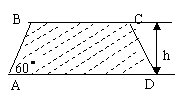
[例1] 建造一条防洪堤,其断面为等腰梯形,腰与底边成角为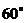 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为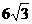 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段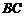 与两腰长的和)要最小.(1)求外周长的最小值,此时防洪堤高h为多少米?(2)如防洪堤的高限制在
与两腰长的和)要最小.(1)求外周长的最小值,此时防洪堤高h为多少米?(2)如防洪堤的高限制在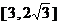 的范围内,外周长最小为多少米?
的范围内,外周长最小为多少米?
[变式]1. 函数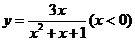 的值域是
的值域是

6.公式法求和 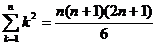
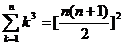
5.裂项相消法求和:把数列的通项拆成两项之差、正负相消剩下首尾若干项。
常见拆项: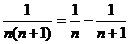
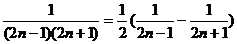
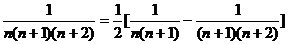
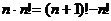
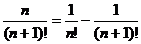
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com