
(1)求证: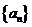 是等比数列;
是等比数列;
(20)设数列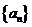 前
前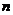 项和为
项和为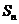 ,且
,且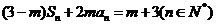 .其中
.其中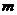 为实常数,
为实常数,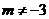 且
且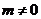 .
.
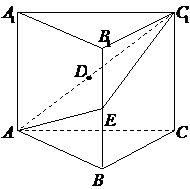 (2)在棱
(2)在棱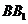 上是否存在点
上是否存在点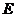 满足
满足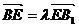 ,使二面角
,使二面角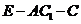 是直二面角?若存在,求出
是直二面角?若存在,求出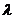 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(1)当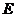 是
是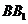 的中点时,证明:
的中点时,证明: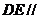 平面
平面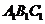 ;
;
(19)(本小题满分12分)如图,直三棱柱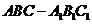 中,
中,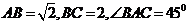 ,
,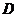 是
是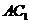 的中点,
的中点,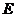 是侧棱
是侧棱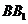 上的一个动点.
上的一个动点.
(Ⅱ)当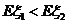 时,求
时,求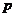 的取值范围.
的取值范围.
(Ⅰ)求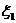 、
、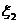 的概率分布和数学期望
的概率分布和数学期望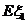 、
、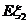 ;
;
(理)现有甲、乙两个项目,对甲项目每投资十万元,一年后利润是1.2万元、1.18万元、1.17万元的概率分别为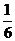 、
、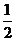 、
、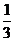 ;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是
;已知乙项目的利润与产品价格的调整有关,在每次调整中价格下降的概率都是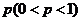 ,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为
,设乙项目产品价格在一年内进行2次独立的调整,记乙项目产品价格在一年内的下降次数为 ,对乙项目每投资十万元,
,对乙项目每投资十万元, 取0、1、2时,一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量
取0、1、2时,一年后相应利润是1.3万元、1.25万元、0.2万元.随机变量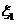 、
、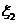 分别表示对甲、乙两项目各投资十万元一年后的利润.
分别表示对甲、乙两项目各投资十万元一年后的利润.
(2)试判断最少需要几秒钟, 、
、 能同时到达点
能同时到达点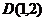 ?并求在最短时间内同时到达的概率.
?并求在最短时间内同时到达的概率.
(1)求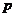 和
和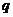 的值;
的值;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com