
7、.解:(1)设等比数列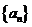 的公比为
的公比为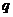 .
.
则由等比数列的通项公式 得
得 ,
,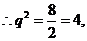
又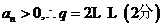
 数列
数列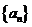 的通项公式是
的通项公式是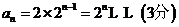 .
.
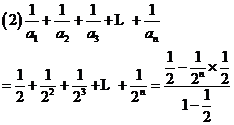
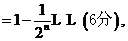
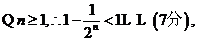
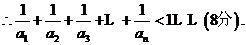
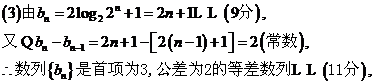
 数列
数列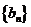 的前100项和是
的前100项和是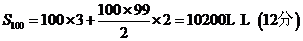
6、解:(Ⅰ)由 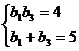 知
知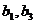 是方程
是方程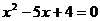 的两根,注意到
的两根,注意到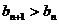 得
得 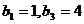 .……2分
.……2分
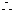
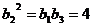 得
得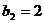 .
.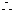
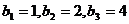
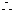 等比数列.
等比数列. 的公比为
的公比为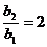 ,
,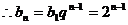 ……4分
……4分
(Ⅱ)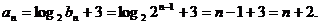 ……5分
……5分
∵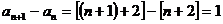 ……7分
……7分
 数列
数列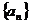 是首相为3,公差为1的等差数列. ……8分
是首相为3,公差为1的等差数列. ……8分
(Ⅲ) 由(Ⅱ)知数列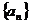 是首相为3,公差为1的等差数列,有
是首相为3,公差为1的等差数列,有
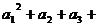 ……
……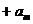 =
=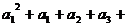 ……
……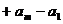
=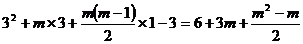 ……10分
……10分 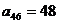
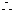
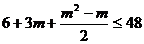 ,整理得
,整理得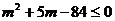 ,解得
,解得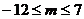 .
. ……11分
……11分
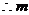 的最大值是7. ……12分
的最大值是7. ……12分
5、解:(I)证明: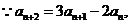
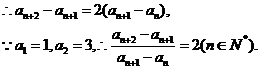
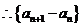 是以
是以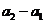
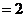 为首项,2为公比的等比数列。
为首项,2为公比的等比数列。
(II)解:由(I)得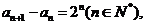
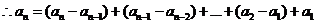
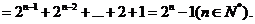
(III)证明: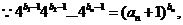
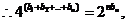
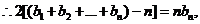 ①
①
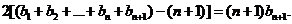 ②
②
②-①,得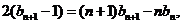 ……10分
……10分
即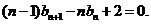 ③
③
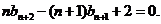 ④
④
④-③,得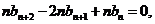
即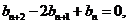
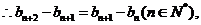
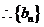 是等差数列.
是等差数列.
21. (Ⅰ)∵函数 f (x) 的图象关于关于直线x=-对称,
∴a≠0,-=-, ∴ b=3a①
∵其图象过点(1,0),则a+b-=0 ②
由①②得a= , b= . 4分
(Ⅱ)由(Ⅰ)得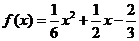 ,∴
,∴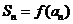 =
=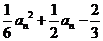
当n≥2时,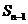 =
=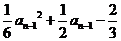 .
.
两式相减得 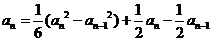
∴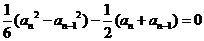 ,∴
,∴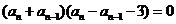

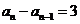 ,∴
,∴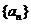 是公差为3的等差数列,且
是公差为3的等差数列,且
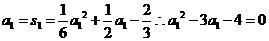
∴a1 = 4 (a1 =-1舍去)∴an =3n+1 9分
(Ⅲ)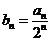 =
=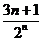 ,
,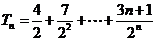 ①
①

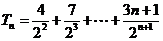 ②
②
①--② 得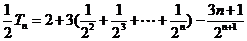
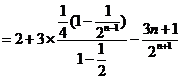
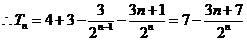
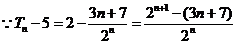 ,
,
(1) 当n=1、2时,Tn -5<0, ∴Tn <5;
(2) 当n=3时,Tn -5=0, ∴ Tn =5;
(3) 当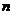 ≥ 4时,记 h (x)
= 2x+1-(3x+7), h ' (x)= 2x+1ln2-3,
≥ 4时,记 h (x)
= 2x+1-(3x+7), h ' (x)= 2x+1ln2-3,
当x >3时,有:h'(x)>23+1ln2-3=23×2×ln2-3=8ln22-3=8ln4-3>8-3>0,
则h(x)在(3, +¥)上单调递增,∴ 当n≥4时,2n+1-(3n+7)>0 ∴Tn -5>0, ∴ Tn >5
综上:当n≤2, Tn<5;当n=3, Tn=5;当n≥4, Tn>5. 14分
3、q 的最大值为 , 此时x=0,∴ 点P的坐标为(0,±). 14分
2、解:(1)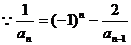 ,
,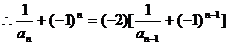 ,
,
又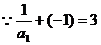 ,∴数列
,∴数列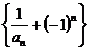 是首项为
是首项为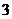 ,公比为
,公比为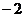 的等比数列.
的等比数列.
(2)依(Ⅰ)的结论有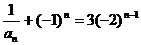 ,即
,即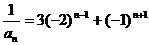 .
.
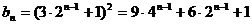 .
.
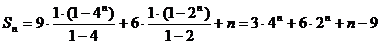 .
.
(3)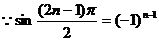 ,又由(Ⅱ)有
,又由(Ⅱ)有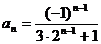
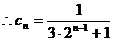 .
.
则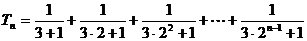
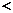 (
( 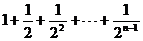 ) =
) = 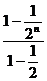
=( 1-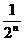 )<∴ 对任意的
)<∴ 对任意的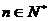 ,
,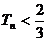 .
.
1、(1) 解法一:由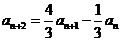 ,得
,得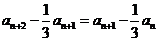 ,
,
∴数列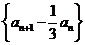 是常数列,
是常数列,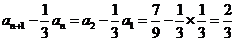 ,
,
即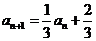 ,得
,得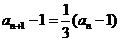 .
.
∴数列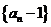 是首项为
是首项为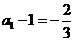 ,公比为
,公比为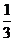 的等比数列,
的等比数列,
∴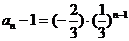 ,故数列
,故数列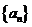 的通项公式为
的通项公式为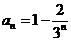 . …………5分
. …………5分
解法二:由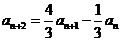 ,得
,得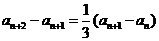 ,
,
∴数列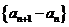 是首项为
是首项为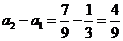 ,公比为
,公比为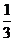 的等比数列,
的等比数列,
∴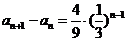 .
.
∴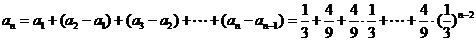
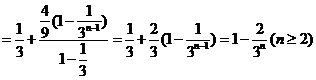 (*)
(*)
当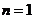 时,
时,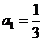 也适合(*),故数列
也适合(*),故数列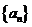 的通项公式为
的通项公式为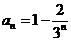 . ………5分
. ………5分
解法三:由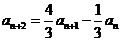 ,得
,得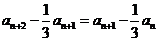 ,
,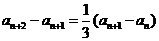 .
.
∴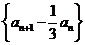 是常数列,
是常数列,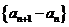 是首项为
是首项为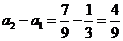 ,公比为
,公比为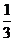 的等比数列.
的等比数列.
∴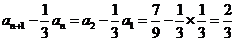 ,且
,且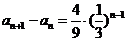 .
.
由上式联立消去 ,解得:
,解得: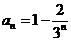 为数列
为数列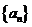 的通项公式. …………5分
的通项公式. …………5分
解法四:由已知,有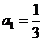 ,
,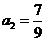 ,
,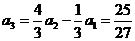 ,从而猜想:
,从而猜想: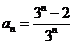 .
.
下用第二数学归纳法证明:
① 当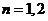 时,结论显然成立.
时,结论显然成立.
② 假设当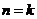 和
和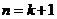 时结论成立,即
时结论成立,即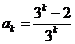 ,
,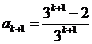 ,
,
则当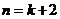 时,
时,
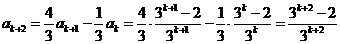 ,即当
,即当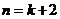 时结论也成立.
时结论也成立.
综上,数列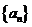 的通项公式为
的通项公式为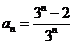 .
…………5分
.
…………5分
(2) 解: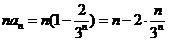 .
.
设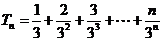 , ①
, ① 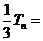
 . ②
. ②
①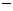 ②得:
②得: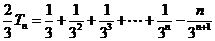
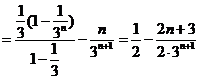 ,
,
∴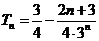 .
.
故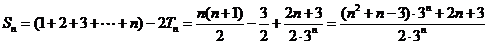 . …9分
. …9分
(3) 证: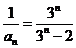 .
.
∵不等式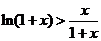 对
对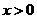 成立,令
成立,令 ,得
,得 ,即
,即
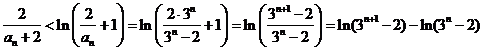 . 于是
. 于是
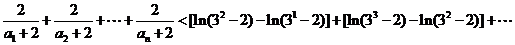
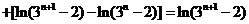 .
.
∴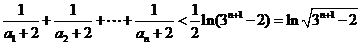 .
…………14分
.
…………14分
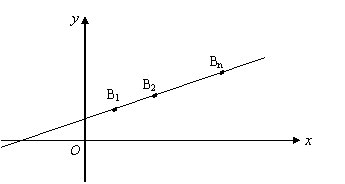
11、(2009番禺)已知点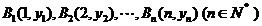 在直线
在直线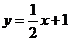 上,点
上,点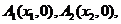
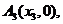 ……,
……,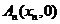 顺次为
顺次为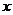 轴上的点,其中
轴上的点,其中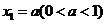 ,对于任意
,对于任意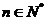 ,点
,点 构成以
构成以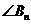 为顶角的等腰三角形, 设
为顶角的等腰三角形, 设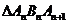 的面积为
的面积为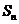 .
.
(1)
证明:数列 是等差数列;
是等差数列;
(2)
求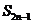 ;(用
;(用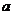 和
和 的代数式表示)
的代数式表示)
(3)
 设数列
设数列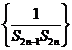 前
前 项和为
项和为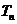 ,判断
,判断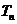 与
与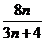 (
(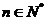 )的大小,并证明你的结论;
)的大小,并证明你的结论;
祥细答案:
10、(2009广东六校一)已知数列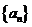 的首项
的首项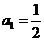 ,前
,前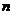 项和
项和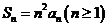 .
.
(Ⅰ)求数列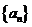 的通项公式;
的通项公式;
(Ⅱ)设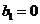 ,
,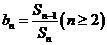 ,
,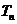 为数列
为数列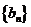 的前
的前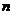 项和,求证:
项和,求证: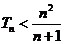 .
.
9、(2009潮南)在数列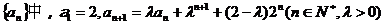
(1) 求数列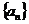 的通项公式;
的通项公式;
(2) 求数列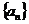 的前n项和
的前n项和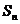 ;
;
(3) 证明存在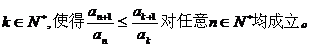
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com