
4.平面向量的基本定理
如果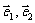 是一个平面内的两个不共线向量,那么对这一平面内的任一向量
是一个平面内的两个不共线向量,那么对这一平面内的任一向量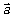 ,有且只有一对实数
,有且只有一对实数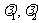 使:
使: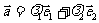 其中不共线的向量
其中不共线的向量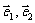 叫做表示这一平面内所有向量的一组基底.
叫做表示这一平面内所有向量的一组基底.
3.两个向量共线定理:
向量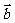 与非零向量
与非零向量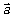 共线
共线 有且只有一个实数
有且只有一个实数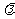 ,使得
,使得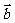 =
=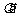 。
。
2.向量的运算
(1)向量加法
求两个向量和的运算叫做向量的加法.
设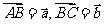 ,则
,则 +
+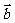 =
=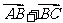 =
=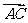 。
。
规定:
(1) ;
;
(2)向量加法满足交换律与结合律;
向量加法的“三角形法则”与“平行四边形法则”
(1)用平行四边形法则时,两个已知向量是要共始点的,和向量是始点与已知向量的始点重合的那条对角线,而差向量是另一条对角线,方向是从减向量指向被减向量。
(2) 三角形法则的特点是“首尾相接”,由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和;差向量是从减向量的终点指向被减向量的终点.
当两个向量的起点公共时,用平行四边形法则;当两向量是首尾连接时,用三角形法则。
向量加法的三角形法则可推广至多个向量相加: 
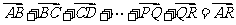 ,但这时必须“首尾相连”。
,但这时必须“首尾相连”。
(2)向量的减法 
①相反向量:与 长度相等、方向相反的向量,叫做
长度相等、方向相反的向量,叫做 的相反向量.
的相反向量.
记作 ,零向量的相反向量仍是零向量。关于相反向量有: (i)
,零向量的相反向量仍是零向量。关于相反向量有: (i)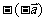 =
= ;
; 
(ii)  +(
+( )=(
)=( )+
)+ =
=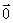 ;(iii)若
;(iii)若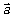 、
、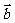 是互为相反向量,则
是互为相反向量,则 =
=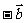 ,
,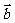 =
= ,
, +
+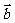 =
=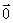 。
。
②向量减法
向量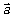 加上
加上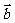 的相反向量叫做
的相反向量叫做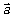 与
与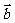 的差,
的差,
记作: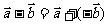 .求两个向量差的运算,叫做向量的减法.
.求两个向量差的运算,叫做向量的减法.
③作图法: 可以表示为从
可以表示为从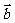 的终点指向
的终点指向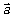 的终点的向量(
的终点的向量(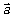 、
、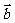 有共同起点)。
有共同起点)。
(3)实数与向量的积
①实数λ与向量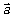 的积是一个向量,记作λ
的积是一个向量,记作λ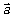 ,它的长度与方向规定如下:
,它的长度与方向规定如下:
(Ⅰ)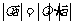 ;
;
(Ⅱ)当 时,λ
时,λ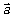 的方向与
的方向与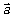 的方向相同;当
的方向相同;当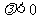 时,λ
时,λ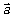 的方向与
的方向与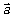 的方向相反;当
的方向相反;当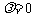 时,
时,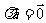 ,方向是任意的。
,方向是任意的。
②数乘向量满足交换律、结合律与分配律.
1.向量的概念
①向量
既有大小又有方向的量。向量一般用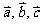 ……来表示,或用有向线段的起点与终点的大写字母表示,如:
……来表示,或用有向线段的起点与终点的大写字母表示,如: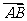 .几何表示法
.几何表示法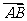 ,
, ;坐标表示法
;坐标表示法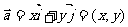 。向量的大小即向量的模(长度),记作|
。向量的大小即向量的模(长度),记作|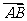 |.即向量的大小,记作|
|.即向量的大小,记作| |。
|。
向量不能比较大小,但向量的模可以比较大小.
②零向量
长度为0的向量,记为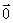 ,其方向是任意的,
,其方向是任意的,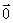 与任意向量平行.零向量
与任意向量平行.零向量 =
=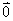
 |
| |=0。由于
|=0。由于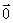 的方向是任意的,且规定
的方向是任意的,且规定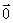 平行于任何向量,故在有关向量平行(共线)的问题中务必看清楚是否有“非零向量”这个条件。(注意与0的区别)
平行于任何向量,故在有关向量平行(共线)的问题中务必看清楚是否有“非零向量”这个条件。(注意与0的区别)
③单位向量
模为1个单位长度的向量,向量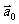 为单位向量
为单位向量 |
|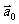 |=1。
|=1。
④平行向量(共线向量)
方向相同或相反的非零向量。任意一组平行向量都可以移到同一直线上,方向相同或相反的向量,称为平行向量,记作 ∥
∥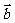 。由于向量可以进行任意的平移(即自由向量),平行向量总可以平移到同一直线上,故平行向量也称为共线向量。
。由于向量可以进行任意的平移(即自由向量),平行向量总可以平移到同一直线上,故平行向量也称为共线向量。
数学中研究的向量是自由向量,只有大小、方向两个要素,起点可以任意选取,现在必须区分清楚共线向量中的“共线”与几何中的“共线”、的含义,要理解好平行向量中的“平行”与几何中的“平行”是不一样的.
⑤相等向量
长度相等且方向相同的向量.相等向量经过平移后总可以重合,记为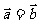 。大小相等,方向相同
。大小相等,方向相同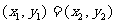
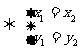 。
。
本讲内容属于平面向量的基础性内容,与平面向量的数量积比较出题量较小。以选择题、填空题考察本章的基本概念和性质,重点考察向量的概念、向量的几何表示、向量的加减法、实数与向量的积、两个向量共线的充要条件、向量的坐标运算等。此类题难度不大,分值5~9分。
预测2010年高考:
(1)题型可能为1道选择题或1道填空题;
(2)出题的知识点可能为以平面图形为载体表达平面向量、借助基向量表达交点位置或借助向量的坐标形式表达共线等问题。
(1)平面向量的实际背景及基本概念
通过力和力的分析等实例,了解向量的实际背景,理解平面向量和向量相等的含义,理解向量的几何表示;
(2)向量的线性运算
①通过实例,掌握向量加、减法的运算,并理解其几何意义;
②通过实例,掌握向量数乘的运算,并理解其几何意义,以及两个向量共线的含义;
③了解向量的线性运算性质及其几何意义.
(3)平面向量的基本定理及坐标表示
①了解平面向量的基本定理及其意义;
②掌握平面向量的正交分解及其坐标表示;
③会用坐标表示平面向量的加、减与数乘运算;
④ 理解用坐标表示的平面向量共线的条件.
26.解:单摆的振动周期公式为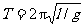 ,据题意l=Lsina ,
,据题意l=Lsina ,
所以A球振动的周期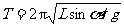 .
.
设球B自由下落的时间为t,则它击中A球下落的高度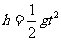 ,
,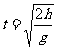
球A经过平衡位置,接着返回到平衡位置的时间为半个周期,即 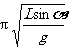
B球能击中A球的时间应为A球做简谐振动的半周期的整数倍,
即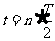 故
故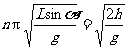
则B球下落的高度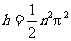 Lsina ,其中n=1,2,3…
Lsina ,其中n=1,2,3…
25.解:本题在分析时要联系牛顿第二定律和机械能的相关知识进行分析。在放物体前其最大回复力为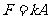 ,振动的机械能为
,振动的机械能为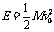 。
。
(1)放上物体m后,一起振动的最大加速度大小为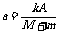 ,对物体而言,所需要的回复力是M施于的静摩擦力,则放上时加速度最大,所需的静摩擦力亦最大,设最大静摩擦力大小为
,对物体而言,所需要的回复力是M施于的静摩擦力,则放上时加速度最大,所需的静摩擦力亦最大,设最大静摩擦力大小为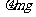 ,则当满足
,则当满足 时,两者可一起振动,即
时,两者可一起振动,即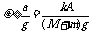 。
。
(2)当两者一起振动时,机械能守恒,过平衡位置时,弹簧恢复原长,弹性势能为零,则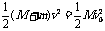 ,
,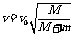 ,物体和振子在最大位移处,动能为零,势能最大,这个势能与没有放物体前相同,所以弹簧的最大形变是不变的,即振幅仍为A。
,物体和振子在最大位移处,动能为零,势能最大,这个势能与没有放物体前相同,所以弹簧的最大形变是不变的,即振幅仍为A。
24.因为圆弧的半径远远大于AB弧长,小球在槽内的摆动可以看为简谐振动,同时小球在沿AD的方向上做匀速直线运动。由于摆动具有周期性,所以小球的速度有通解。
沿AD方向:小球的运动时间t=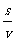
又小球在摆动,要到达D点,则t=nT=n·2π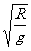 (n=0、1、2、3……)
(n=0、1、2、3……)
得出v=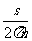
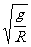 (n=0、1、2、3……)
(n=0、1、2、3……)
23.解:最高点木块不脱离弹簧,则振动的最高点不超过弹簧的原长,即A≤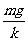 ,从而有:
,从而有: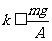
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com