
21、解:(Ⅰ)已知式即 ,故
,故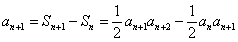 .
.
因为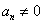 ,当然
,当然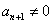 ,所以
,所以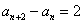
 .
.
由于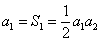 ,且
,且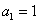 ,故
,故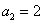 .
.
于是 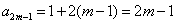 ,
,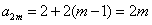 ,
,
所以 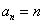
 .
……………4分
.
……………4分
(Ⅱ)由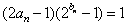 ,得
,得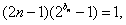
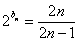 ,
,
故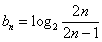 .从而
.从而 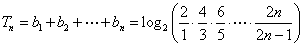 .
.
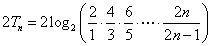
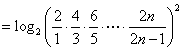
因此
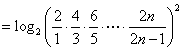
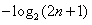

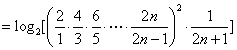 .
.
设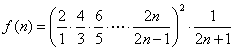 ,
,
则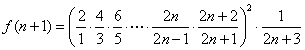 ,
,
故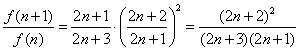
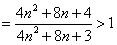 ,
,
注意到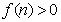 ,所以
,所以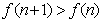 .
.
特别地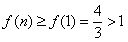 ,从而
,从而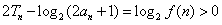 .
.
所以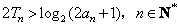 .
………………12分
.
………………12分
22.(本小题满分12分)已知函数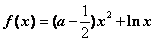 .(
.( )
)
(Ⅰ)当 时,求
时,求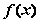 在区间[1,e]上的最大值和最小值;
在区间[1,e]上的最大值和最小值;
(Ⅱ)若在区间(1,+∞)上,函数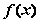 的图象恒在直线
的图象恒在直线 下方,求
下方,求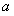 的取值范围.
的取值范围.

 又平面
又平面 平面
平面
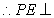 平面
平面 。
。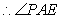 就是
就是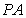 与平面
与平面 所成的角。……6分
所成的角。……6分
 ………………………7分
………………………7分
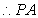 与平面
与平面 所成的角的正切值为
所成的角的正切值为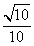 ………8分
………8分
(3)解:当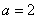 时,
时,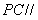 平面
平面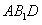 ………9分由
………9分由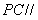 平面
平面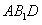 ,
,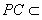 平面
平面 ,平面
,平面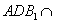 平面
平面
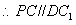 ,又
,又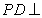 平面
平面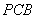 ,
,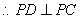 ,因而
,因而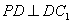 …10分又
…10分又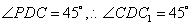 即
即 是正方形,
是正方形,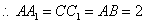 …………………12分
…………………12分
21、(本小题满分12分)
已知数列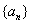 的前
的前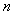 项和为
项和为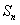 ,且
,且 ,其中
,其中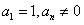 .
.
(Ⅰ)求数列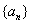 的通项公式;
的通项公式;
(Ⅱ)设数列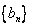 满足
满足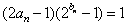 ,
,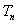 为
为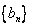 的前
的前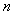 项和,求证:
项和,求证:
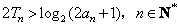 ;
;
20.(本小题满分12分)
在如图组合体中, 是一个长方体,
是一个长方体,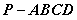 是一个四棱锥。
是一个四棱锥。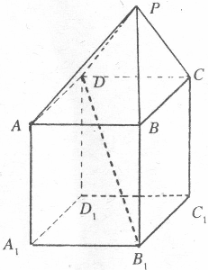
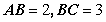 ,
,
点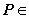 平面
平面 ,且
,且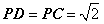 。
。
(1)证明: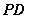
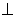 平面
平面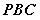 ;
;
(2)求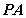 与平面
与平面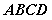 所成的角的正切值;
所成的角的正切值;
(3)若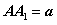 ,当
,当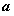 为何值时,
为何值时,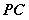
 平面
平面 。
。
19、(本题满分12分)
若点P是椭圆 上一点,
上一点,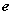 为离心率,
为离心率,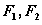 分别为椭圆的左右焦点,若
分别为椭圆的左右焦点,若
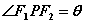 ,求证
,求证
18.(本小题满分12分)
某公司拟资助三位大学生自主创业,现聘请两位专家,独立地对每位大学生的创业方案进行评审.假设评审结果为“支持”或“不支持”的概率都是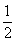 .若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助.求:
.若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助.求:
(1)该公司的资助总额为零的概率
(2)该公司资助总额超过15万元的概率
17、(本小题满分10分)
在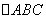 中,
中,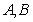 为锐角,角
为锐角,角 所对应的边分别为
所对应的边分别为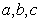 ,且
,且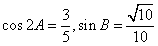
(I)求 的值;(II)若
的值;(II)若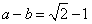 ,求
,求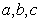 的值。
的值。
16.直线 和圆
和圆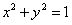 交于点A、B,以
交于点A、B,以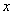 轴的正方向为始边,OA为终边(O是坐标原点)的角为
轴的正方向为始边,OA为终边(O是坐标原点)的角为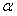 ,OB为终边的角为
,OB为终边的角为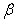 ,那么
,那么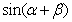 = .
= .
15. 设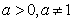 ,函数
,函数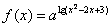 有最大值,则不等式
有最大值,则不等式 的解集为 。
的解集为 。
14、已知点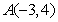 ,
,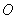 是直角坐标原点,点
是直角坐标原点,点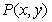 满足
满足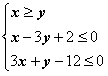 ,则
,则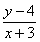 的取值范围是________。
的取值范围是________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com