122．导数公式你记清了吗？(理)对复合函数的该如何求导？(①和与差的导数等于导数的和与差；②乘法的求导：前导后不导，后导前不导，中间是正号；③除法的求导：分母平方要记牢，上导下不导，下导上不导，中间是负号)(理) 复合函数的求导问题是个难点，要分清中间变量与复合关系，复合函数求导法则，像链条一样，必须一环一环套下去，而不能丢掉其中的一环. 防止漏掉一部分或漏掉符号造成错误.必须正确分析复合函数是由哪些基本函数经过怎样的顺序复合而成的，分清其间的复合关系.

121．导数的概念你理解了吗？导数有些什么应用。(理)定积分的概念与应用应注意.

① 了解函数单调性和导数的关系；能利用导数研究函数的单调性，会求函数的单调区间，对多项式函数一般不超过三次. ② 了解函数在某点取得极值的必要条件和充分条件；会用导数求函数的极大值、极小值，对多项式函数一般不超过三次；会求闭区间上函数的最大值、最小值，对多项式函数一般不超过三次.

120．(理) 怎样选择应用基底(不设直角坐标系)？如何建立直角坐标系及坐标系？

运用空间向量解题，应注意选取适当的基底对相关的向量进行合理的分解。基底的选取应注意以下两点：一是三个向量不共面；二是这三个向量中两两的夹角都可求，一般在四面体、正方体和长方体中，都是以从同一个顶出发的三条棱所在向量作为基底的。

119．(理)利用空间向量解决立体几何的步骤是什么？运用空间向量的坐标运算解决几何问题时，一般步骤为：(1)建立适当建立空间直角坐标系；(2)计算出相关点的坐标；(3)写出向量的坐标，(4)结合公式进行论证、计算；(5)转化为几何结论。在建立空间直角坐标系时，必须要牢牢抓住相交于同一点的两两垂直的三条直线，要在题目中所给出的垂直关系(如线线垂直、线面垂直与面面垂直等)，同时要注意所建立的直角坐标系必须是右手直角坐标系，在此坐标系下，点的坐标的写出，可根据图中有关线段的长度，也可以根据向量的运算。

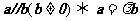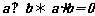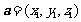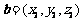118．利用空间向量的坐标运算可将立体几何中有关平行、垂直、夹角、距离等问题转化为向量的坐标运算，如(1)判断线线平行或诸点共线，可以转化为证；(2)证明线线垂直，转化为证，若，，则转化为计算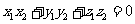；(3)在计算异面直线所成的角(或线面角、二面角)时，转化为求向量的夹角，利用公式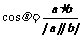；(4)在立体几何中求线段的长度问题时，转化为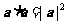，或利用空间两点间的距离公式。

117．若A(x₁,y₁), B(x₂,y₂)是二次曲线C：F(x,y)=0的弦的两个端点，则F(x₁,y₁)=0 且F(x₂,y₂)=0。涉及弦的中点和斜率时，常用点差法作F(x₁,y₁)-F(x₂,y₂)=0求得弦AB的中点坐标与弦AB的斜率的关系。

116．过抛物线y²=2px(p>0)焦点的弦交抛物线于A(x₁,y₁),B(x₂,y₂)，则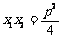，，焦半径公式|AB|=x₁+x₂+p。

115．通径是抛物线的所有焦点弦中最短的弦。

114．在用圆锥曲线与直线联立求解时，消元后得到的方程中要注意：二次项的系数是否为零？判别式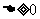的限制．(求交点，弦长，中点，斜率，对称，存在性问题都在下进行)。

113．在利用圆锥曲线统一定义解题时，你是否注意到定义中的定比的分子分母的顺序？