
13.你注意到指数函数与对数函数互为反函数了吗?你知道互为反函数的两个函数图像之间有何关系吗?(关于直线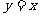 对称) .
对称) .
12.抽象函数的单调性、奇偶性一定要紧扣函数性质利用单调性、奇偶性的定义求解。同时,要领会借助函数单调性利用不等关系证明等式的重要方法:f(a)≥b且f(a)≤bÛf(a)=b
11.你知道函数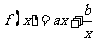
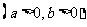 的有关性质吗?
的有关性质吗?
①定义域:
②奇偶性:奇函数;
③单调性:在区间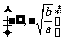 和
和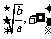 上单调递增,
上单调递增,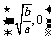 和
和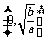 上单调递减;
上单调递减;
 ④ 在定义域内的极值是
④ 在定义域内的极值是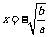 时有极大值,
时有极大值,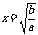 时有极小值。在指定的定义域内的极值或最值要根据单调性或图象来判断。
时有极小值。在指定的定义域内的极值或最值要根据单调性或图象来判断。
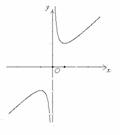
⑤ 记住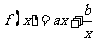
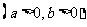 的图象的草图。
的图象的草图。
⑥ 要能够类比得出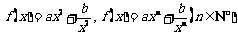 的有关性质.
的有关性质.
10.根据定义证明函数的单调性时,规范格式是什么?(取值, 作差, 判正负.)用导数研究函数单调性时,一定要注意 “
“ >0(或
>0(或 <0)是该函数在给定区间上单调递增(减)的必要条件。
<0)是该函数在给定区间上单调递增(减)的必要条件。
9.求二次函数的最值问题时你注意到x的取值范围了吗?“方程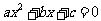 有实数解”转化为“
有实数解”转化为“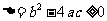 ”,你是否注意到“
”,你是否注意到“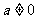 ”(除解决二次方程的有关问题时要注意之外,在解决直线与圆锥曲线的位置关系时,也常常遇到),在题目中没有指出是“二次”函数,方程,不等式时,就要分类讨论
”(除解决二次方程的有关问题时要注意之外,在解决直线与圆锥曲线的位置关系时,也常常遇到),在题目中没有指出是“二次”函数,方程,不等式时,就要分类讨论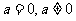 的不同情况,不要忽略
的不同情况,不要忽略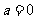 的讨论.
的讨论.
8.记住函数的几个重要性质:
(1)关于对称性.
函数图象的对称轴和对称中心举例
|
函 数 满 足 的 条 件 |
对称轴(中心) |
满足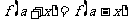 的函数 的函数 的图象 的图象[或 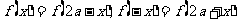 ] ] |
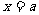 |
满足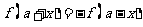 的函数 的函数 的图象 的图象[或 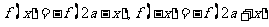 ] ] |
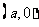 |
满足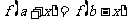 的函数 的函数 的图象 的图象 |
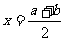 |
满足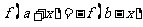 的函数 的函数 的图象 的图象 |
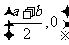 |
满足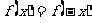 的函数 的函数 的图象(偶函数) 的图象(偶函数) |
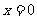 |
满足 的函数 的函数 的图象(奇函数) 的图象(奇函数) |
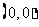 |
满足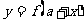 与 与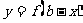 的两个函数的图象 的两个函数的图象 |
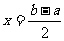 |
满足 与 与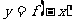 的两个函数的图象 的两个函数的图象 |
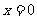 |
满足 与 与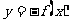 的两个函数的图象 的两个函数的图象 |
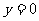 |
(2) 关于奇偶性与单调性的关系.
① 如果奇函数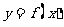 在区间
在区间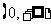 上是递增的,那么函数
上是递增的,那么函数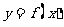 在区间
在区间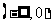 上也是递增的;
上也是递增的;
② 如果偶函数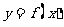 在区间
在区间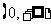 上是递增的,那么函数
上是递增的,那么函数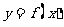 在区间
在区间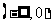 上是递减的;
上是递减的;
(3) 关于单调性.
①证明函数的单调性的方法为定义法和导数法.
②关于复合函数的单调性.
如果函数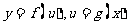 在区间
在区间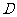 上定义,
上定义,
若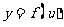 为增函数,
为增函数, 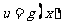 为增函数,则
为增函数,则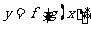 为增函数;
为增函数;
若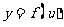 为增函数,
为增函数, 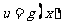 为减函数,则
为减函数,则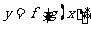 为减函数;
为减函数;
若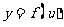 为减函数,
为减函数, 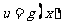 为减函数,则
为减函数,则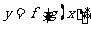 为增函数;
为增函数;
若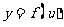 为减函数,
为减函数, 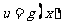 为增函数,则
为增函数,则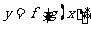 为减函数;
为减函数;
③关于分段函数的单调性.
若函数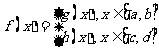 ,
,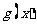 在区间
在区间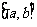 上是增函数,
上是增函数, 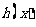 在区间
在区间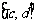 上是增函数,则
上是增函数,则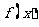 在区间
在区间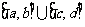 上不一定是增函数,若使得
上不一定是增函数,若使得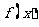 在区间
在区间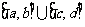 上一定是增函数,需补充条件:
上一定是增函数,需补充条件: 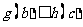
(4) 关于图象变换.
|
平移 变 换 |
向左移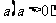 个单位 个单位向右移 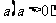 个单位 个单位向上移 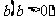 个单位 个单位向下移 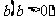 个单位 个单位按向量 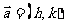 平移 平移 |
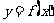 的图象→ 的图象→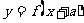 的图象 的图象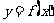 的图象→ 的图象→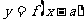 的图象 的图象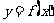 的图象→ 的图象→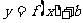 的图象 的图象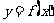 的图象→ 的图象→ 的图象 的图象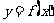 的图象→ 的图象→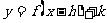 的图象 的图象 |
|
伸 缩 变 换 |
每点纵标伸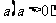 倍 倍每点横标伸 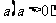 倍 倍 |
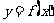 的图象→ 的图象→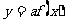 的图象 的图象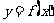 的图象→ 的图象→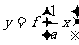 的图象 的图象 |
|
绝对 值 变换 |
关于  轴对称 轴对称将  轴下方图象翻上 轴下方图象翻上 |
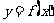 的图象→ 的图象→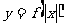 的图象 的图象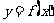 的图象→ 的图象→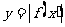 的图象 的图象 |
(5) 关于周期性.
函数的对称性与周期性的关系
函数关系(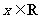 ) ) |
周期 |
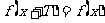 |
 |
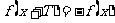 |
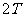 |
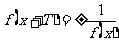 |
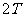 |
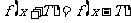 |
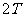 |
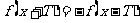 |
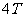 |
 |
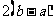 |
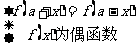 |
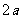 |
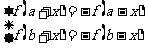 |
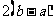 |
 |
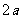 |
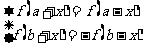 |
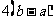 |
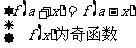 |
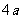 |
 |
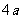 |
(6) 关于奇偶性.
|
②若奇函数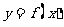 在
在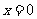 处有定义,则
处有定义,则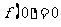 ;对于偶函数的定义常可用到下面的形式:
;对于偶函数的定义常可用到下面的形式: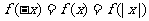 .
.
③任何一个定义域关于原点对称的函数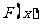 ,总可以表示为一个奇函数
,总可以表示为一个奇函数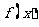 和一个偶函数
和一个偶函数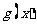 的和,其中
的和,其中
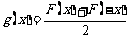 .
.
(7) 求函数的解析式,特别是解应用题的函数式时,一定要注明定义域.
(8) 求方程或不等式的解集,或者求定义域,值域时,要按要求写成集合的形式.
7.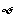 是任何集合的子集,是任何非空集合的真子集。
是任何集合的子集,是任何非空集合的真子集。
6.反演律: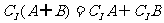 ,
,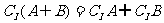 .
.
5.对于含有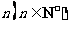 个元素的有限集合
个元素的有限集合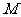 ,其子集, 真子集,非空子集, 非空真子集的个数依次为
,其子集, 真子集,非空子集, 非空真子集的个数依次为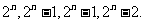
4.当集合中的元素是字母时,你是否注意到了元素的互异性?(如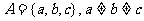 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com