
4.下列各项中,标点符号使用不规范的一项是( )
A.小河对岸三四里外是浅山,好似细浪微波,线条柔和,宛延起伏,连接着高高的远山。
B.陶潜说过:“亲戚或余悲,他人亦已歌,死去何所道,托体同山阿”。倘能如此,这也就够了。
C.除了他能去,还有谁呢?你吗?你能去吗?我看你不能去吧?
D.如果想对中国古代史有个初步的了解,可以参阅《四库全书简明目录》(1957年古典文学出版社出版了铅印本。此目录包括经、史、子、集)。
3. 下列句子中,加点的词语使用不恰当的一项是( )
A.对于这个问题,我们不要再争论了,事实胜于雄辩,还是让事实来说话吧。
B.北大教授季羡林深受大众尊敬,媒体也不断给他扣帽子,冠以“国学大师”“学界泰斗”和“国宝”等称号。
C.在同一所学校,同一个班级,由同一位老师授课,学生们的水平却参差不齐,这个现象不能不引起我们的思考。
D.起初是他创建了这家公司,后来公司又毁在他手里,真是成也萧何,败也萧何。
2.下列每组词语中,有两个错别字的一组是( )
A. 自栩 座右铭 迫不急待 休养生息
B. 精粹 化妆品 以儆效尤 提纲挈领
C. 气慨 拌脚石 卓而不群 穷兵渎武
D. 嬉戏 副食品 穿流不息 不肖子孙
1.下列各组词语中加点字的读音,有错误的一组是( )
A.谥号(shì) 讪笑(shàn) 泥古不化(nì) 踽踽独行(jǔ)
B.掮客(qián) 靓妆(jìng) 余勇可贾(gǔ) 自怨自艾(yì)
C.薄荷(bò) 太监(jiàn) 济济一堂(jì) 差强人意(chā)
D.渐染(jiān) 蒙骗(mēng) 乳臭未干(xiù) 曲高和寡(hè)
1 若α是三角形的一个内角,且sinα=
若α是三角形的一个内角,且sinα=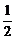 ,则α等于( )
,则α等于( )
A.30° B.30°或150° C.60° D.120°或60°
2 若0<α<2π,则满足5sin2α-4=0的α有( )
若0<α<2π,则满足5sin2α-4=0的α有( )
A.1个 B.2个 C.3个 D.4个
3 满足sin2x=
满足sin2x=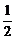 的x的集合是( )
的x的集合是( )
A.{x|x=kπ+(-1)k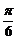 ,k∈Z}B.{x|x=2kπ±
,k∈Z}B.{x|x=2kπ±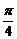 ,k∈Z}
,k∈Z}
C.{x|x=kπ+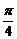 ,k∈Z} D.{x|x=
,k∈Z} D.{x|x=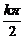 +
+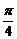 ,k∈Z}
,k∈Z}
4 若sin2x=-
若sin2x=-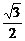 ,且0<x<2π,则x=
,且0<x<2π,则x=

5 若sin2x=
若sin2x=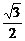 ,则x=
,则x=

6 若sinα=sin
若sinα=sin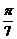 ,α∈R,则α=
,α∈R,则α= 
7 已知sinx+cosx=
已知sinx+cosx=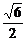 ,x∈(0,
,x∈(0,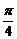 ),求x
),求x
8 已知sin2x=sin2
已知sin2x=sin2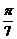 ,求x
,求x
9 已知方程sinx+cosx=m在[0,π]内总有两个不同的解,求m的范围
已知方程sinx+cosx=m在[0,π]内总有两个不同的解,求m的范围
例1 (1)已知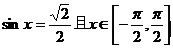 ,求x
,求x
解: 在
在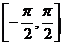 上正弦函数是单调递增的,且符合条件的角只有一个
上正弦函数是单调递增的,且符合条件的角只有一个
∴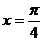 (即
(即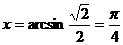 )
)
(2)已知
解: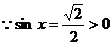 ,
,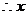 是第一或第二象限角
是第一或第二象限角
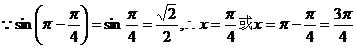
即(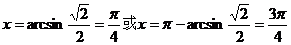 )
)
(3)已知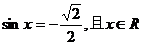
解: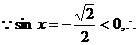 x是第三或第四象限角
x是第三或第四象限角
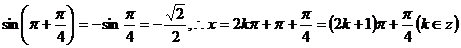
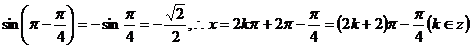
(即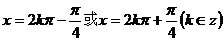 或
或
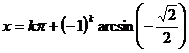 )
)
这里用到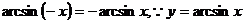 是奇函数
是奇函数
例2 (1)已知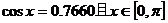 ,求
,求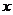
解:在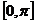 上余弦函数
上余弦函数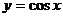 是单调递减的,且符合条件的角只有一个
是单调递减的,且符合条件的角只有一个

(2)已知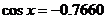 ,且
,且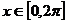 ,求x的值
,求x的值
解: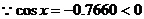 ,
,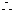 x是第二或第三象限角
x是第二或第三象限角
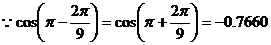
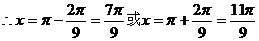
(3)已知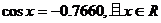 ,求x的值
,求x的值
解:由上题: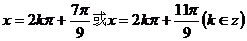

介绍:∵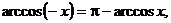
∴上题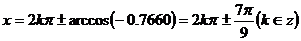
简单理解反正弦,反余弦函数的意义:
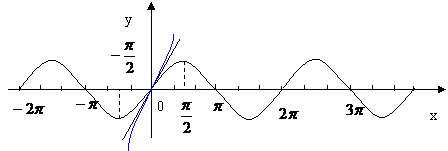 由
由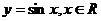
1°在R上无反函数
2°在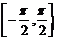 上,
上,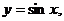 x与y是一一对应的,且区间
x与y是一一对应的,且区间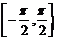 比较简单
比较简单
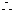 在
在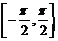 上,
上,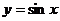 的反函数称作反正弦函数,
的反函数称作反正弦函数,
记作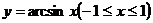 ,(奇函数)
,(奇函数)
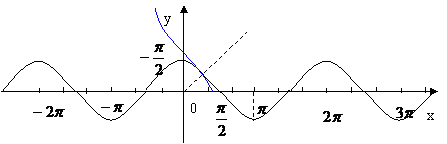 同理,由
同理,由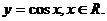
在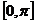 上,
上,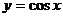 的反函数称作反余弦函数,
的反函数称作反余弦函数,
记作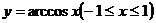
已知三角函数求角:
首先应弄清:已知角求三角函数值是单值的;已知三角函数值求角是多值的
诱导公式一(其中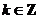 ): 用弧度制可写成
): 用弧度制可写成
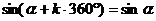
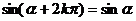
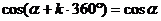
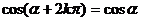
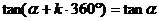
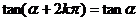
公式二: 用弧度制可表示如下:
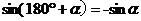
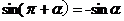
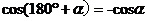
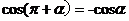
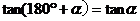
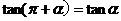
公式三: 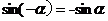
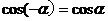
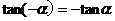
公式四: 用弧度制可表示如下:
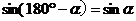
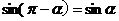
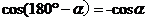
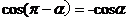
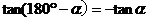
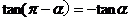
公式五: 用弧度制可表示如下:
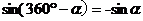
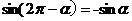
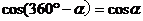
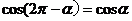
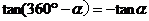
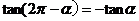
诱导公式6:
sin(90° -a) = cosa, cos(90° -a) = sina
tan(90° -a) = cota, cot(90° -a) = tana
sec(90° -a) = csca, csc(90° -a) = seca
诱导公式7:
sin(90° +a) = cosa,
cos(90° +a) = -sina
tan(90° +a) = -cota, cot(90° +a) = -tana
sec(90° +a) = -csca, csc(90°+a) = seca
诱导公式8:
sin(270° -a) = -cosa,
cos(270° -a) = -sina
tan(270° -a) = cota, cot(270° -a) = tana
sec(270° -a) = -csca, csc(270°-a) = seca
诱导公式9:
sin(270° +a) = -cosa, cos(270° +a) = sina
tan(270° +a) = -cota, cot(270° +a) = -tana
sec(270° +a) = csca, csc(270°+a) = -seca
诱导公式应用广泛,不仅已知任意一个角,(角必须属于这个函数的定义域),可以求出它的三角函数值,而且反过来,如果已知一个三角函数值,也可以求出与它对应的角.这就是本节课的主要内容.
20.(本小题满分16分)已知函数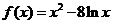 ,
,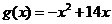 .
.
(1) 求函数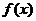 在点
在点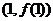 处的切线方程;
处的切线方程;
(2) 若函数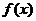 与
与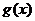 在区间
在区间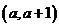 上均为增函数,求
上均为增函数,求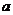 的取值范围;
的取值范围;
(3) 若方程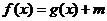 有唯一解,试求实数
有唯一解,试求实数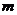 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com