
求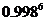 的近似值,使误差小于
的近似值,使误差小于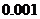 .
.
解: ,
,
展开式中第三项为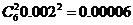 ,小于
,小于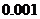 ,以后各项的绝对值更小,可忽略不计,∴
,以后各项的绝对值更小,可忽略不计,∴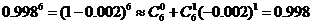 ,
,
一般地当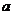 较小时
较小时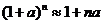

2.因为二项式定理中的字母可取任意数或式,所以在解题时根据题意,给字母赋值,是求解二项展开式各项系数和的一种重要方法

(1)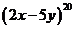 的展开式中二项式系数的和为 ,各项系数的和为
,二项式系数最大的项为第
项;
的展开式中二项式系数的和为 ,各项系数的和为
,二项式系数最大的项为第
项;
(2)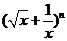 的展开式中只有第六项的二项式系数最大,则第四项为 .
的展开式中只有第六项的二项式系数最大,则第四项为 .
(3)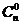 +
+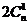 +
+ +
+
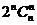
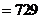 ,则
,则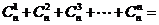 ( )
( )
A. B.
B. C.
C.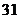 D.
D.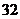
(4)已知: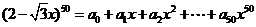 ,
,
求: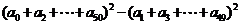 的值
的值 
答案:(1) ,
, ,
, ;
;
(2)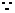 展开式中只有第六项的二项式系数最大,
展开式中只有第六项的二项式系数最大,
∴ 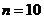 ,
, 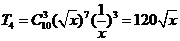 ;
;
(3)A.
例1.在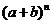 的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和
的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和
证明:在展开式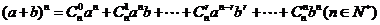 中,令
中,令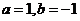 ,则
,则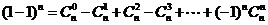 ,
,
即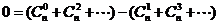 ,
,
∴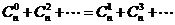 ,
,
即在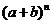 的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
说明:由性质(3)及例1知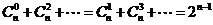 .
.
例2.已知 ,求:
,求:
(1)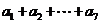 ; (2)
; (2)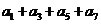 ; (3)
; (3)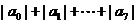 .
.
解:(1)当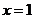 时,
时,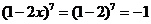 ,展开式右边为
,展开式右边为

∴
 ,
,
当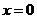 时,
时,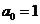 ,∴
,∴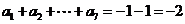 ,
,
(2)令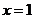 ,
, 
 ①
①
令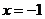 ,
, ②
②
①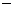 ② 得:
② 得: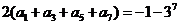 ,∴
,∴ 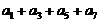
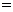
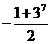 .
.
(3)由展开式知: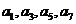 均为负,
均为负,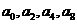 均为正,
均为正,
∴由(2)中①+② 得: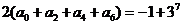 ,
,
∴  ,
,
∴

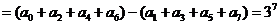

例3.求(1+x)+(1+x)2+…+(1+x)10展开式中x3的系数
解: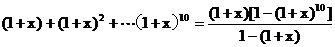
= ,
,
∴原式中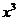 实为这分子中的
实为这分子中的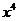 ,则所求系数为
,则所求系数为

例4.在(x2+3x+2)5的展开式中,求x的系数
解:∵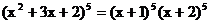
∴在(x+1)5展开式中,常数项为1,含x的项为 ,
,
在(2+x)5展开式中,常数项为25=32,含x的项为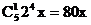
∴展开式中含x的项为 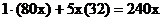 ,
,
∴此展开式中x的系数为240
例5.已知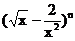 的展开式中,第五项与第三项的二项式系数之比为14;3,求展开式的常数项
的展开式中,第五项与第三项的二项式系数之比为14;3,求展开式的常数项
解:依题意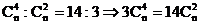
∴3n(n-1)(n-2)(n-3)/4!=4n(n-1)/2!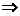 n=10
n=10
设第r+1项为常数项,又
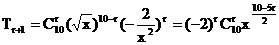
令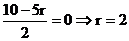 ,
,
 此所求常数项为180
此所求常数项为180
1 二项式系数表(杨辉三角)
二项式系数表(杨辉三角)
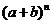 展开式的二项式系数,当
展开式的二项式系数,当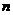 依次取
依次取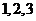 …时,二项式系数表,表中每行两端都是
…时,二项式系数表,表中每行两端都是 ,除
,除 以外的每一个数都等于它肩上两个数的和
以外的每一个数都等于它肩上两个数的和 
2.二项式系数的性质:

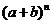 展开式的二项式系数是
展开式的二项式系数是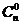 ,
,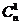 ,
,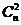 ,…,
,…,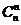 .
. 可以看成以
可以看成以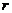 为自变量的函数
为自变量的函数
定义域是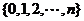 ,例当
,例当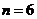 时,其图象是
时,其图象是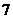 个孤立的点(如图)
个孤立的点(如图)
(1)对称性.与首末两端“等距离”的两个二项式系数相等(∵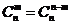 ).
).
直线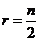 是图象的对称轴.
是图象的对称轴.
(2)增减性与最大值.∵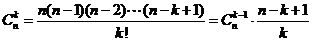 ,
,
∴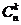 相对于
相对于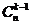 的增减情况由
的增减情况由 决定,
决定,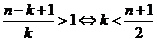 ,
,
当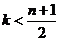 时,二项式系数逐渐增大.由对称性知它的后半部分是逐渐减小的,且在中间取得最大值;
时,二项式系数逐渐增大.由对称性知它的后半部分是逐渐减小的,且在中间取得最大值;
当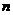 是偶数时,中间一项
是偶数时,中间一项 取得最大值;当
取得最大值;当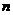 是奇数时,中间两项
是奇数时,中间两项 ,
,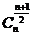 取得最大值.
取得最大值.
(3)各二项式系数和:
∵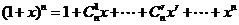 ,
,
令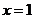 ,则
,则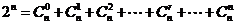

3. 求常数项、有理项和系数最大的项时,要根据通项公式讨论对
求常数项、有理项和系数最大的项时,要根据通项公式讨论对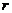 的限制;求有理项时要注意到指数及项数的整数性
的限制;求有理项时要注意到指数及项数的整数性 
2.二项展开式的通项公式: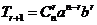


1.二项式定理及其特例:
(1)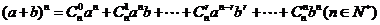 ,
,
(2)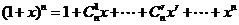 .
.
23、在下列横线上补写出相应名篇名句。(10分,每空1分)
文人学者为了表明志向寄托情怀,常从名篇佳句中选字取意,命名书屋或居室。如柳亚子有一书房曰“磨剑室”,即取意于贾岛的诗句“十年磨一剑,霜刃未曾试”。填写出下列(1)(2)(3)处书屋名称所取意的名句。
(1)“十驾斋”取意于 , 。
(2)“锲斋”取意于 , 。
(3)“人镜庐”取意于 , 。
(4)于是废先王之道, , 。(《过秦论》)
(5)王安石《桂枝香•金陵怀古》中:“ , , 。”化用了杜牧《泊秦淮》的诗句:“商女不知亡国恨,隔江犹唱《后庭花》。”
(6)五步一楼,十步一阁, , 。(《阿房宫赋》)
(7)欧阳修在《伶官传序》中就后唐庄宗耽溺于伶人而丧国的史实,告诫后人应记住:“ , 。”
(8)杜甫在《登岳阳楼》中由个人身世转写国事危难,感伤涕零的诗句是:“ , 。”
(9)《梦游天姥吟留别》中李白表现诗人蔑视权贵的诗句是: , !”
(10) 多情的文人总是用自己的感情为景物染色。王勃笔下的秋笔触虽明媚,却有几分落寞:“时维九月,序属三秋。 , 。”
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com