
2.带电粒子在电场中的运动可能是: 平衡、直线加速或减速、偏转
1.研究对象:
①基本粒子:电子、质子、α粒子等,因为质量很小,所以重力比电场力小得多,所以重力可以忽略不计(但质量不可忽略)
②带电颗粒:尘埃、液滴、小球等,因为质量较大,重力不可忽略。
2. 电场能的性质:
(1)电势: ①定义式:
②点电荷: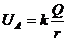
③匀强电场:
④电势是标量,有正负,理论上:无穷远处
实际上:大地或人为确定
(2)电势差: ①定义式: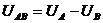
②点电荷:
③匀强电场: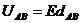
④电势差是标量,有正负,大小与零电势无关
(3)电势能:①定义式: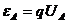
②点电荷: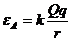
③匀强电场: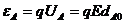
④电势能是标量,有正负,理论上:无穷远处
实际上:大地或人为确定
(4) 电场力的功:电场力做功,做正功,电势能减少;
做负功,电势能增加。
①
一般式: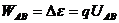
②
匀强电场: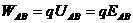
注意:使用公式计算将各量的正负符号代入。
*若只有电场力做功,电荷动能与电势能之间相或转化而总能量保持不变。
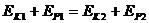
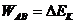
(5) 等势面的特点:(电势相等的点连成的面)
①在同一势面上的任何两点间移动电荷,电场力不做功.
②等势面一定与电力线垂直,即与场强方向垂直.
③电力线由电势高的等势面指向电势低的等势面.
④等势面的疏密表示场强的大小.(密-场强大)
⑤处于静电平衡的导体是一个等势体,它的表面是一个等势面.
⑥任意两个等势面都不会相交.
注意:电场线、等势面是人们假想出来的线和面。
1. 力的性质
(1)
电场强度:①定义式: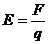 (矢量)
(矢量)
方向:正电荷的受力方向。
②决定式: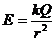 (适用于点电荷)
(适用于点电荷)
③在匀强电场中,E处处大小相等方向相同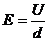
④电场的叠加: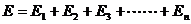 (失量和)
(失量和)
(2)电场力:①定义式: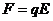 (矢量)
(矢量)
②点电荷: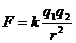
③在匀强电场中, 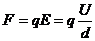
例:
(3)电力线的特点
①从正电荷出发,终至于负电荷,不闭合、不中断。
②每一点的切线方向为该点的场强方向。
③电力线越密,场强就越大。
④电力线不会相交,不是电荷的运动轨迹。
⑤只有直线, 电荷会沿电力线运动。
电荷会沿电力线运动。
⑥匀强电场,一组方向相同,疏密相同的平行线。
2. 库仑定律: 在真空中的两个点电荷间的相互作用力,跟它们电量的乘积成正比,跟它们距离的平方成反比,作用力的方向在它们的连线上。
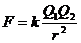
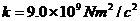
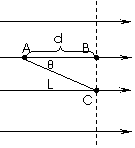
例:已知两个固定点电荷,
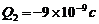 ,它们之间的距离为20厘米,引入第三个点电荷(1)若使
,它们之间的距离为20厘米,引入第三个点电荷(1)若使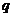 静止?求其所放位置、电量、电性(2)若
静止?求其所放位置、电量、电性(2)若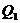
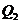 都为自由点电荷,放入第三个点电荷均平衡,求
都为自由点电荷,放入第三个点电荷均平衡,求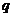 的电性;
的电性;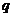 的位置;
的位置;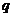 的电量。
的电量。
小结:真空的三个自由点电荷达平衡时的特点:
(1) 三点共线,两同夹异,两大夹小。
(2) 第三者靠近原来电量较小的,由它的受力平衡求间距;
(3) 由前两者电量的平衡求第三个点电荷的电量。
1. 电荷守恒定律:电荷既不会创生,也不会消失,它只能从一个物体上(或某一部分)转移到另一物体(或部分),而电荷的总量保持不变。
6.在平面内,先将一个多边形以点 为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为
为位似中心放大或缩小,使所得多边形与原多边形对应线段的比为 ,并且原多边形上的任一点
,并且原多边形上的任一点 ,它的对应点
,它的对应点 在线段
在线段 或其延长线上;接着将所得多边形以点
或其延长线上;接着将所得多边形以点
 为旋转中心,逆时针旋转一个角度
为旋转中心,逆时针旋转一个角度 ,这种经过和旋转的图形变换叫做旋转相似变换,记为
,这种经过和旋转的图形变换叫做旋转相似变换,记为 ,其中点
,其中点 叫做旋转相似中心,
叫做旋转相似中心, 叫做相似比,
叫做相似比, 叫做旋转角.
叫做旋转角.
(1)填空:
①如图1,将 以点
以点 为旋转相似中心,放大为原来的2倍,再逆时针旋转
为旋转相似中心,放大为原来的2倍,再逆时针旋转 ,得到
,得到 ,这个旋转相似变换记为
,这个旋转相似变换记为 ( , );
( , );
②如图2, 是边长为
是边长为 的等边三角形,将它作旋转相似变换
的等边三角形,将它作旋转相似变换 ,得到
,得到 ,则线段
,则线段 的长为
的长为  ;
;
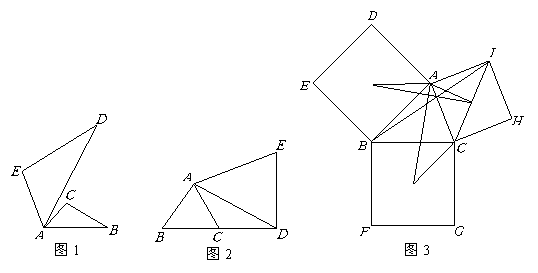 (2)如图3,分别以锐角三角形
(2)如图3,分别以锐角三角形 的三边
的三边 ,
, ,
, 为边向外作正方形
为边向外作正方形 ,
, ,
, ,点
,点 ,
, ,
, 分别是这三个正方形的对角线交点,试分别利用
分别是这三个正方形的对角线交点,试分别利用 与
与 ,
, 与
与 之间的关系,运用旋转相似变换的知识说明线段
之间的关系,运用旋转相似变换的知识说明线段 与
与 之间的关系.
之间的关系.
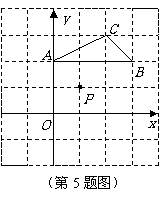
5.如图,在平面直角坐标系中,点 的坐标分别为
的坐标分别为
 .
.
(1)请在图中画出 ,使得
,使得 与
与 关于点
关于点 成中心对称;
成中心对称;
(2)若一个二次函数的图象经过(1)中 的三个顶点,求此二次函数的关系式.
的三个顶点,求此二次函数的关系式.
4.如图, 中
中 ,
, ,
, .
.
(1)将 向右平移
向右平移 个单位长度,
个单位长度,
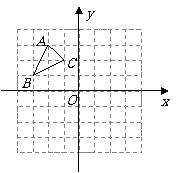 画出平移后的
画出平移后的 ;
;
(2)画出 关于
关于 轴对称的
轴对称的 ;
;
(3)将 绕原点
绕原点 旋转
旋转 ,画出旋转后的
,画出旋转后的 ;
;
(4)在 ,
, ,
, 中,
中,
 ______与
______与 ______成轴对称,对称轴是______;
______成轴对称,对称轴是______;
 ______与
______与 ______成中心对称,对称中心的坐标是______.
______成中心对称,对称中心的坐标是______.
3.在平面直角坐标系中,直线 过点M(3,0),且平行于
过点M(3,0),且平行于 轴.
轴.
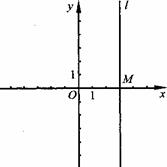 (1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-l,O),C(-1,2),△ABC关于
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-l,O),C(-1,2),△ABC关于 轴的对称图形是△A1B1C1,△A1B1C1关于直线
轴的对称图形是△A1B1C1,△A1B1C1关于直线 的对称
的对称
图形是△A2B2C1,写出△A2B2C1的三个顶点的坐标;
(2)如果点 的坐标是(
的坐标是( ,0),其中
,0),其中 ,点P关于
,点P关于
 轴的对称点是
轴的对称点是 ,点
,点 关于直线
关于直线 的对称点是
的对称点是 ,
,
求 的长.
的长.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com