
3.与中山站相比,昆仑站所在的地点 ( )
A.年降雪量较大 B. 气压较高 C.年太阳辐射较强 D.年均风力较小
答案 D
2.昆仑站与中山站的直线距离约为
A.820千米 B.1020千米 C.1220千米 D.1420千米
答案 C
(09辽宁文宋综)南极中山站( ,
,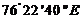 )时间(区时)2009年2月2日9时25分,我国在南极最高点附近建立的昆仑站(
)时间(区时)2009年2月2日9时25分,我国在南极最高点附近建立的昆仑站(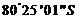 ,
,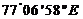 )正式开站。根据此完成1-3题。
)正式开站。根据此完成1-3题。
1.昆仑站正式开站时,北京时间为2009年2月2日 ( )
A.5时25分 B.6时25分 C.12时25分 D.13时25分
答案 C
2009高考题
40.已知函数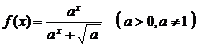 .
.
(1)求 及
及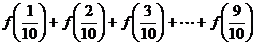 的值;
的值;
(2)是否存在自然数 ,使
,使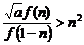 对一切
对一切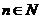 都成立,若存在,求出自然数
都成立,若存在,求出自然数 的最小值;不存在,说明理由;
的最小值;不存在,说明理由;
(3)利用(2)的结论来比较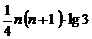 和
和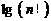
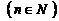 的大小.
的大小.
解(1)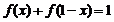 ;
;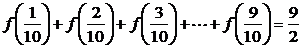 .
.
(2)假设存在自然数 ,使
,使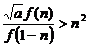 对一切
对一切 都成立.
都成立.
由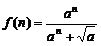 ,
, 得
得 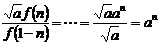 ,
,
当 时,不等式
时,不等式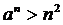 显然不成立.
显然不成立.
当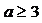 时,
时,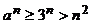 ,
,
当n=1时,显然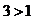 ,
,
当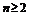 时,
时, =
= 成立,则
成立,则 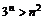 对一切
对一切 都成立.
都成立.
所以存在最小自然数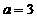 。
。
(3). 由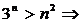
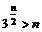 (
(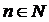 ),所以
),所以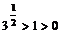 ,
,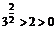 ,……,
,……,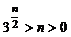 ,
,
相乘得 ,∴
,∴

 成立.
成立.
39.过P(1,0)做曲线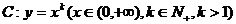 的切线,切点为Q1,设Q1在
的切线,切点为Q1,设Q1在 轴上的投影为P1,又过P1做曲线C的切线,切点为Q2,设Q2在
轴上的投影为P1,又过P1做曲线C的切线,切点为Q2,设Q2在 轴上的投影为P2,…,依次下去得到一系列点Q1、Q2、Q3、…、Qn的横坐标为
轴上的投影为P2,…,依次下去得到一系列点Q1、Q2、Q3、…、Qn的横坐标为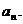 求证:
求证:
(Ⅰ)数列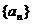 是等比数列;
是等比数列;
(Ⅱ) ;
;
(Ⅲ)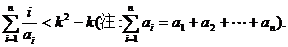
解:(Ⅰ)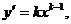 若切点是
若切点是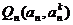 ,
,
则切线方程为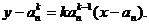
当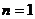 时,切线过点P(1,0)即
时,切线过点P(1,0)即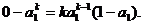 得
得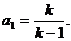
当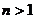 时,切线过点
时,切线过点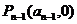 即
即 得
得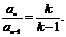
∴数列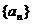 是首项为
是首项为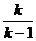 ,公比为
,公比为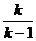 的等比数列.
的等比数列. 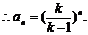 …6分
…6分
(Ⅱ)

(Ⅲ)记 ,
,
则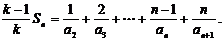
两式相减

38.对数列 ,规定
,规定 为数列
为数列 的一阶差分数列,其中
的一阶差分数列,其中 。对正整数k,规定
。对正整数k,规定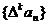 为
为 的k阶差分数列,其中
的k阶差分数列,其中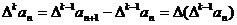 。
。
(1) 若数列 首项
首项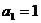 ,且满足
,且满足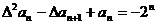 ,求数列
,求数列 的通项公式;
的通项公式;
(2) 对(1)中的数列 ,是否存在等差数列
,是否存在等差数列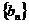 ,使得
,使得 对一切正整数
对一切正整数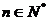 都成立?若存在,求数列
都成立?若存在,求数列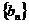 的通项公式;若不存在,请说明理由;
的通项公式;若不存在,请说明理由;
(3) 令 ,设
,设 ,若
,若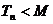 恒成立,求最小的正整数M的值。
恒成立,求最小的正整数M的值。
解(1)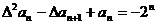 而
而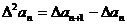 可得
可得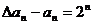
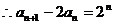 ,
, ,
,
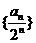 是首项为
是首项为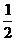 ,公差为
,公差为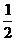 的等差数列,
的等差数列,
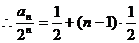 ,
,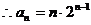
(2) 即:
即:
而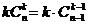

= 故可得
故可得
 存在等差数列
存在等差数列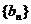 ,
, 使
使 对一切正整数
对一切正整数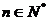 都成立。
都成立。
(3)由(2)知1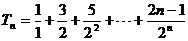 ……… ①
……… ①
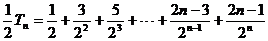 ……… ②
……… ②
①-②得:
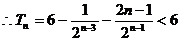
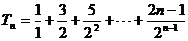 ,
,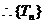 递增 ,且
递增 ,且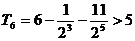 。
。
 满足条件的最小的正整数M的值为6
满足条件的最小的正整数M的值为6
37.如图所示,已知A,B为椭圆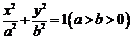 和双曲线
和双曲线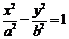 的公共顶点。P,Q分别为双曲线和椭圆上不同于A、B的动点,且有
的公共顶点。P,Q分别为双曲线和椭圆上不同于A、B的动点,且有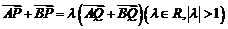 ,设AP,BP,AQ,BQ的斜率分别为
,设AP,BP,AQ,BQ的斜率分别为 。
。
(Ⅰ)求证; ;
;
(Ⅱ)设 分别为椭圆和双曲线的右焦点,
分别为椭圆和双曲线的右焦点,
若
PF2∥QF1 ,求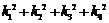 的值。
的值。
解(Ⅰ):设点P,Q的坐标分别为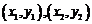
则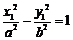 ,即
,即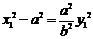
所以
类似地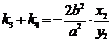
设O为原点,则
∵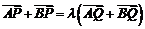 ∴
∴ , ∴三点O,P,Q共线
, ∴三点O,P,Q共线
∴ ,由①②得
,由①②得
(Ⅱ)证明:因点Q在椭圆上,有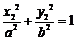
由 知
知
即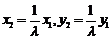 ,从而
,从而 ……③
……③
又点P在双曲线上,有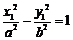 …………④
…………④
由③④解得
因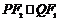 ,∴
,∴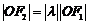 ,故
,故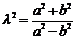
所以
由①得
同理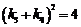
另一方面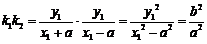
类似地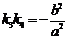
所以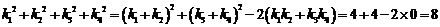
36.已知: =(c,0)(c>0),
=(c,0)(c>0),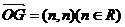 ,
,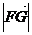 最小值为1.若动点P同时满足下列条件①
最小值为1.若动点P同时满足下列条件① ②
② 其中
其中 ③动点P的轨迹C过点B(0,-1).
③动点P的轨迹C过点B(0,-1).
(1) 求c的值;
(2) 求曲线C的方程;
(3)
过点M(0,2)的直线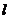 与曲线C的轨迹交于A,B两点,求
与曲线C的轨迹交于A,B两点,求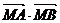 的取值范围.
的取值范围.
解:(1) 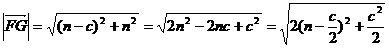 ,
,
当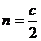 时,
时, 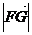 的最小值为1,
的最小值为1,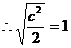 ,
,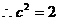 ,
,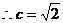 .
.
(2)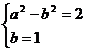 ,
,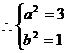 ,
,  曲线C的方程为
曲线C的方程为 .
.
(3)设直线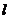 的方程为:
的方程为: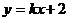 .
.
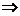
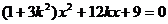 (*)
(*)
由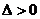 得:
得: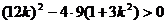
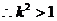
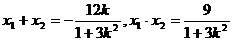

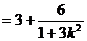 ,又
,又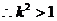 ,
,
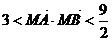 .
.
当k不存在时, 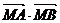 =3,所以
=3,所以 .
.
35.已知一次函数f(x)的图像关于直线x-y=0对称的图像为C,且f(-1)=0,若点(n+1,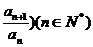 在曲线C上,并有
在曲线C上,并有 。
。
(1) 求曲线C的方程;
(2)
求数列 的通项公式;
的通项公式;
(3)
设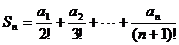 ,若
,若 恒成立,求实数M的取值范围。
恒成立,求实数M的取值范围。
解:(1)设f(x)=kx+b(k 0),则曲线C的方程为
0),则曲线C的方程为 。
。
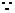 f(-1)=0,
f(-1)=0, -k+b=0
①
-k+b=0
①
又点(n+1,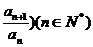 在曲线C上,
在曲线C上,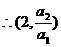 即(2,1)在曲线上。
即(2,1)在曲线上。
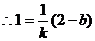 ②
由①②得:k=b=1
②
由①②得:k=b=1
 C:x-y-1=0。
C:x-y-1=0。
(2)点(n+1,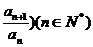 在曲线C上,
在曲线C上,
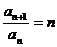 ,而
,而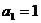 。
。
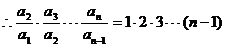 ,
,
(3) 。
。
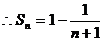 关于n单调增。
关于n单调增。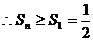 。
。
故 恒成立,则
恒成立,则
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com