
(19)(本题14分)一个袋中有若干个大小相同的黑球、白球和红球。已知从袋中任意摸出1个球,得到黑球的概率是 ;从袋中任意摸出2个球,至少得到1个白球的概率是
;从袋中任意摸出2个球,至少得到1个白球的概率是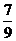 。
。
(Ⅰ)若袋中共有10个球,
(i)求白球的个数;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为 ?
?
(18)(本题14分)如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF,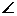 BCF=
BCF=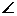 CEF=
CEF= ,AD=
,AD= ,EF=2。
,EF=2。
(Ⅰ)求证:AE//平面DCF;
(17)若 ,且当
,且当 时,恒有
时,恒有 ,则以
,则以 ,b为坐标点P(
,b为坐标点P( ,b)所形成的平面区域的面积等于____________。
,b)所形成的平面区域的面积等于____________。
(15)已知t为常数,函数 在区间[0,3]上的最大值为2,则t=__________。
在区间[0,3]上的最大值为2,则t=__________。
(16)用1,2,3,4,5,6组成六位数(没有重复数字),要求任何相邻两个数字的奇偶性不同,且1和2相邻,这样的六位数的个数是__________(用数字作答)。
(14)如图,已知球O点面上四点A、B、C、D,DA 平面ABC,AB
平面ABC,AB BC,DA=AB=BC=
BC,DA=AB=BC= ,则球O点体积等于___________。
,则球O点体积等于___________。
(13)在△ABC中,角A、B、C所对的边分别为 、b、c
,若
、b、c
,若 ,则
,则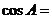 _________________。
_________________。
若 ,则
,则 =______________。
=______________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com