
(II)在(I)的结论下,设 ,求函数
,求函数 的最小值.
的最小值.
已知函数 上是增函数.
上是增函数.
(I)求实数a的取值范围;
21.(本小题共12分)
(2)过圆 上一动点
上一动点 作平行于
作平行于 轴的直线
轴的直线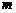 ,设
,设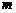 与
与 轴的交点为
轴的交点为 ,若向量
,若向量 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
(1)直线 过点
过点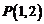 ,且与圆
,且与圆 交于
交于 、
、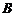 两点,若
两点,若 ,求直线
,求直线 的方程;
的方程;
20. (本小题满分12分) 已知圆 方程为:
方程为: .
.
 19.(本小题满分12分)在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2
19.(本小题满分12分)在三棱锥S-ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2 ,M、N分别为AB、SB的中点。
,M、N分别为AB、SB的中点。
(Ⅰ)证明:AC⊥SB;
(Ⅱ)求二面角N-CM-B的余弦值;
(Ⅲ)求点B到平面CMN的距离。
⑵在⑴的条件下,记抽检的产品件数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
⑴若这箱产品被用户接收的概率是 ,求n的值;
,求n的值;
18. (本小题满分12分)一厂家向用户提供的一箱产品共10件,其中有n件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子),若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com