由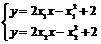  ② 

y ?? 2 = 2x₂ (x ? x₂) ， 即：y = 2x₂ x ? + 2   

y ? ? 2 = 2x₁ (x ? x₁) ，即：y = 2x₁x ?   

    （2）解：∵A，B两点坐标为A (x₁，+ 2)，B (x₂，)，∴l₁，l₂的方程分别为：

    【解析】（1）证明：对y = x² + 2求导得：y′= 2x，则y′即l₁，l₂的斜率分别为2x₁，2x₂．又由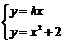得x² ? kx + 2 = 0 ①

    ∴x₁ + x₂ = k即2x₁ + 2x₂ = 2k．∴2x₁，k，2x₂成等差数列．

21．（本小题满分13分）已知函数y = kx与y = x² + 2 (x≥0)的图象相交于不同两点A (x₁，y₁)，B (x₂，y₂)，l₁，l₂分别是y = x² + 2 (x≥0)的图象在A、B两点的切线，M、N分别是l₁、l₂与x轴的交点，P为l₁与l₂的交点．

    （1）求证：直线l₁，y = kx，l₂的斜率成等差数列；

    （2）求l₁与l₂交点P的轨迹方程；

    （3）是否存在实数k使得△ABP的面积最大？若存在，请求出k的值；若不存在，请说明理由．

综上可知，m的取值范围为            ……13分

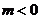  ∴，即  ∴        ……12分

当<0，即m>-1 时，

∴3m+4>0 ,即  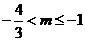 ∴      ……9分