
2.给加点字注音。(2分)
畸形( ) 执拗( ) 哂笑( ) 健脾( )
1.抄写下面的句子(2分)(书写规范漂亮可得3分)
勿忘历史,珍惜和平,铸剑为犁,共同发展!

(图1) (图2)
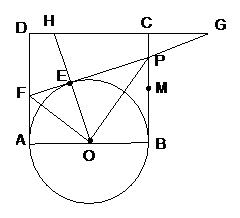
25、如图(1)正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不运动到点M,点C),以AB为直径作⊙O,过点P作⊙O的切线交AD于点F,切点为E。
(1)求四边形CDFP的周长;
(2)设BP=x,AF=y,求y关于x的函数解析式,并写出自变量x的取值范围;
(3)延长DC,FP相交于点G,连接OE并延长交直线DC于H〔如图(2)〕。问是否存在点P,使ㄓEFO∽ㄓEHG(其中ㄓEFO顶点 E、F、O与ㄓEHG顶点E、H、G
为对应点)?如果存在,试求(2)中x和y的值;如果不存在,请说明理由。
(1)求证:当AC=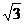 时,PC与⊙O相切;
时,PC与⊙O相切;
(2)在PC与⊙O相切的条件下,求sin∠APD的值。
24、如图,已知AB=2,AB、CD是⊙O的两条直径,M为弧AB的中点,C在弧MB上运动,点P在AB的延长上,且PC=AC,作CE⊥AP于E,连结DP交⊙O于F。
23、某商店以2400元购进某种盒装茶叶,第一个月每盒按进价增加20ㄇ作为售价,售出50盒。第二个月每盒以低于进价5元作为售价,售完余下的茶叶。在整个买卖过程中盈利350元。求每盒茶叶的进价。
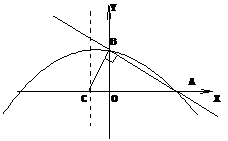 22、如图,抛物线与直线
22、如图,抛物线与直线
 都经过坐标轴的正半轴上A,B两点,该抛物线的对称轴x=-1,与x轴交于点C,且∠ABC=90°求:
都经过坐标轴的正半轴上A,B两点,该抛物线的对称轴x=-1,与x轴交于点C,且∠ABC=90°求:
(1)直线AB的解析式;
(2)抛物线的解析式。
 21、一船从西向东航行,航行到灯塔C处,测得海岛B在北偏东60°方向,该船继续向东航行到达灯塔D处时,测得海岛B在北偏东45°方向,若灯塔C、D间的距离是10海里,海岛B周围12海里有暗礁,问该船继续航行(沿原方向)有无触礁的危险?
21、一船从西向东航行,航行到灯塔C处,测得海岛B在北偏东60°方向,该船继续向东航行到达灯塔D处时,测得海岛B在北偏东45°方向,若灯塔C、D间的距离是10海里,海岛B周围12海里有暗礁,问该船继续航行(沿原方向)有无触礁的危险?
|