
2、0.002006用科学记数法表示为 ( )
1、下列各点中,在第三象限的点是 ( )
A.(2,4) B.(2,-4) C.(-2,4) D.(-2,-4))
⑶请你选定某一时刻,求出经过三点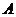 、
、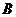 、
、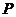 的抛物线的解析式。
的抛物线的解析式。
⑵试判断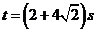 时,以点
时,以点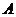 为圆心,
为圆心,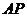 为半径的圆与以点
为半径的圆与以点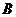 为圆心、
为圆心、 半径的圆的位置关系;除此之外
半径的圆的位置关系;除此之外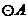 与
与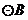 还有其他位置关系吗?如果有,请求出
还有其他位置关系吗?如果有,请求出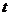 的取值范围。
的取值范围。
⑴在运动开始后的每一时刻一定存在以点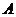 、
、 、
、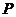 为顶点的三角形和以点
为顶点的三角形和以点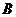 、
、 、
、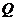 为顶点的三角形吗?如果存在,那么以点
为顶点的三角形吗?如果存在,那么以点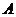 、
、 、
、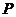 为顶点的三角形和以点
为顶点的三角形和以点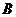 、
、 、
、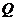 为顶点的三角形相似吗?以点
为顶点的三角形相似吗?以点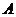 、
、 、
、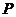 为顶点的三角形和以点
为顶点的三角形和以点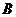 、
、 、
、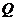 为顶点的三角形会同时成为等腰直角三角形吗?请分别说明理由。
为顶点的三角形会同时成为等腰直角三角形吗?请分别说明理由。
27、在平面直角坐标系中(单位长度: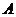 、
、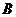 两点的坐标分别为
两点的坐标分别为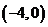 ,
,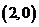 ,点
,点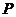 从点
从点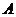 开始以
开始以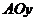 运动,同时点
运动,同时点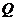 从点
从点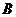 开始以
开始以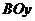 运动。
运动。
⑶点 是第二象限内到
是第二象限内到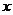 轴、
轴、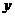 轴的距离的比为5:2的点,如果点
轴的距离的比为5:2的点,如果点 在⑵中的抛物线上,且它与点
在⑵中的抛物线上,且它与点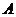 在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点
在此抛物线对称轴的同侧,问:在抛物线的对称轴上是否存在点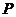 ,使
,使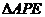 的周长最小?若存在,求出点
的周长最小?若存在,求出点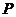 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
⑵点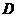 是抛物线与
是抛物线与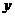 轴的交点,点
轴的交点,点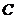 是抛物线上的一点,且以
是抛物线上的一点,且以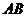 为一底的梯形
为一底的梯形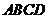 的面积为9,求此抛物线的解析式。
的面积为9,求此抛物线的解析式。
⑴求抛物线与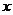 轴的另一个交点
轴的另一个交点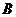 的坐标。
的坐标。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com