（2）       如果将“MN为两圆的内公切线”改成“MN为两圆的外公切线”，其余条件不变，那么∠AMN和∠BNM有怎样的数量关系？请在图（2）中画出图形，并写出你的结论。（不需写出证明过程）

25．已知，如图（1），半径不等的两圆⊙O₁、⊙O₂外离，线段O₁O₂交⊙O₁于A，交⊙O₂于B，MN为两圆的内公切线，切⊙O₁于M，切⊙O₂于N，连结MA、NB。

（1）       请判断∠AMN和∠BNM的数量关系，并证明你的结论；

     （2）当点C运动到什么位置时，四边形CEDF成为正方形？

24． 如图，点D为线段AB的中点，点C为线段AB的垂直平分线上的任意一点，DE⊥AC于点E，DF⊥BC于点F。

求证：（1）CE=CF；

（2）      若抛物线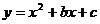过点A、B，求此抛物线的解析式。

（1）      求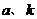的值；

数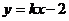的图象与x轴交于点B。

23．已知反比例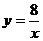函数与一次函数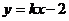的图象都经过点A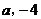（），且一次函

（5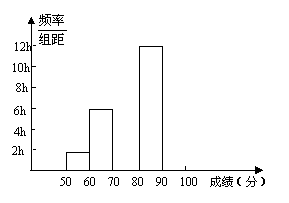）       80～90组的平均分为________，中位数为_______。

分数段

频数

频率

50～60

2

1/15

60～70

6

1/5

70～80

80～90

12

2/5

90～100