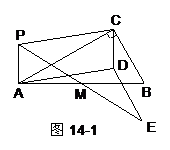
25．如图14－1，P为Rt△ABC所在平面内任意一点(不在直线

AC上)，∠ACB = 90°，M为AB边中点．

操作：以PA、PC为邻边作平行四边形PADC，连续PM并

延长到点E，使ME = PM，连结DE．

探究：⑴请猜想与线段DE有关的三个结论；

⑵请你利用图14－2，图14－3选择不同位置的点P按上述方法操作；

⑶经历⑵之后，如果你认为你写的结论是正确的，请加以证明；

如果你认为你写的结论是错误的，请用图14－2或图14－3加以说明；

(注意：错误的结论，只要你用反例给予说明也得分)

⑷若将“Rt△ABC”改为“任意△ABC”，其他条件不变，利用图14－4操作，并写出与线

段DE有关的结论(直接写答案)．

⑶小明为了通过描点法作出函数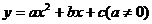的图象，列出表3：

表3：

x

x₁

x₂

x₃

x₄

x₅

x₆

x₇

y

10

50

110

190

290

412

550

由于小明的粗心，表3中有一个y值算错了，请指出算错的y值(直接写答案)．

⑵若将函数“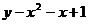”改为“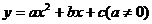”，列出表2：

表2：

x

x₁

x₂

x₃

x₄

x₅

x₆

x₇

y

y₁

y₂

y₃

y₄

y₅

y₆

y₇

其他条件不变，判断s₁、s₂、s₃之间关系，并说明理由；

24．小明为了通过描点法作出函数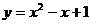的图象，先取自变量x的7个值满足：

x₂－x₁ = x₃－x₂ = … = x₇－x₆ = d，再分别算出对应的y值，列出表1：

   表1：

x

x₁

x₂

x₃

x₄

x₅

x₆

x7

y

1

3

7

13

21

31

43

记m₁ = y₂－y₁，m₂ = y₃－y₂，m₃ = y₄－y₃，m₄ = y₅－y₄，…；s₁ = m₂－m₁，s₂ = m₃－m₂，

s₃ = m₄－m₃，…

⑴判断s₁、s₂、s₃之间关系，并说明理由；

五、解答题和附加题(本题共3小题，24、25题各12分，26题10分，共34分，附加题5分，全卷累积不超过150分，附加题较难，建议考生最后答附加题)

23．如图13－1、图13－2分别是两个相同正方形、正六边形，其中一个正多边形的顶点在另一个正多边形外接圆圆心O处．

⑴求图13－1中，重叠部分面积与阴影部分面积之比；

⑵求图13－2中，重叠部分面积与阴影部分面积之比(直接出答案)；

⑶根据前面探索和图13－3，你能否将本题推广到一般的正n边形情况，(n为大于2的偶数)？若能，写出推广问题和结论；若不能，请说明理由．

22．甲、乙两工程队分别承担一条2千米公路的维修工作，甲队有一半时间每天维修公路x千米，另一半时间每天维修公路y千米．乙队维修前1千米公路是地，每天维修x千米；维修后1千米公路时，每天维修y千米(x≠y)．

⑴求甲、乙两队完成任务需要的时间(用含x、y的代数式表示)；

⑵问甲、乙两队哪队先完成任务？

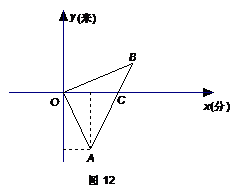求小欣家与学校距离及小欣早晨上学需要的时间．

21．早晨小欣与妈妈同时从家里出发，步行与骑自行车到方向相反的两地上学与上班，图12是他们离家的路程 y (米)与时间 x (分)的函数图象．妈妈骑车走了10分时接到小欣的电话，即以原速骑车前往小欣学校，并与小欣同时到达学校．已知小欣步行速度为每分50米，