考点:组合图形的面积
专题:平面图形的认识与计算
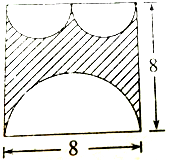
分析:由图可知,阴影部分的面积可由正方形的面积减去3个半圆的面积得到;正方形的边长是8厘米,可以根据正方形的面积=边长×边长求出正方形的面积;较大的半圆的直径是8厘米,先用8厘米除以2求出它的半径,再根据圆的面积公式S=πr2,求出整圆的面积,再除以2就是这个较大半圆的面积;两个较小半圆的直径和是8厘米,用8厘米除以2,求出每个半圆的直径,再除以2即可得出它们的半径;又由于两个半圆是相等的,所以它们的面积和就是一个整圆的面积,再根据圆的面积公式求出整圆的面积,从而得解.
解答:
解:8÷2=4(厘米)
8÷2÷2=2(厘米)
8×8-3.14×42÷2-3.14×22
=64-25.12-12.56
=26.32(平方厘米)
答:阴影部分的面积是26.32平方厘米.
点评:此题考查了正方形的面积及圆形的面积计算,属于基础题,解答本题的关键是求出空白部分的面积,难度一般.