
【题目】已知函数![]() ,设关于
,设关于![]() 的方程
的方程![]() 有
有![]() 个不同的实数解,则
个不同的实数解,则![]() 的所有可能的值为( )
的所有可能的值为( )
A. 3 B. 1或3 C. 4或6 D. 3或4或6
【答案】B
【解析】由已知, ![]() ,令
,令![]() ,解得
,解得![]() 或
或![]() ,则函数
,则函数![]() 在
在![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减,极大值
上单调递减,极大值![]() ,最小值
,最小值![]() .
.
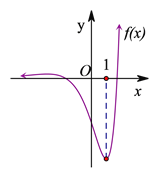
综上可考查方程![]() 的根的情况如下(附函数
的根的情况如下(附函数![]() 图):
图):
(1)当![]() 或
或![]() 时,有唯一实根;
时,有唯一实根;
(2)当![]() 时,有三个实根;
时,有三个实根;
(3)当![]() 或
或![]() 时,有两个实根;
时,有两个实根;
(4)当![]() 时,无实根.
时,无实根.
令![]() ,则由
,则由![]() ,得
,得 ,
,
当![]() 时,由
时,由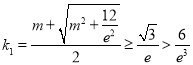 ,
,
符号情况(1),此时原方程有1个根,
由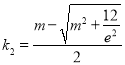 ,而
,而![]() ,符号情况(3),此时原方程有2个根,综上得共有3个根;
,符号情况(3),此时原方程有2个根,综上得共有3个根;
当![]() 时,由
时,由![]() ,又
,又![]() ,
,
符号情况(1)或(2),此时原方程有1个或三个根,
由![]() ,又
,又![]() ,符号情况(3),此时原方程有两个根,
,符号情况(3),此时原方程有两个根,
综上得共1个或3个根.
综上所述, ![]() 的值为1或3.故选B.
的值为1或3.故选B.


 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com