
【题目】如图,在四棱椎![]() 中,底面
中,底面![]() 为菱形,
为菱形, ![]() 为
为![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)若![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,求三棱椎
,求三棱椎![]() 的体积.
的体积.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1) 连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,由底面
,由底面![]() 为菱形,可知点
为菱形,可知点![]() 为
为![]() 的中点,根据三角形中位线定理可得
的中点,根据三角形中位线定理可得 ![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]() 平面
平面![]() ;(2)根据相似三角形的性质以及勾股定理可求出
;(2)根据相似三角形的性质以及勾股定理可求出![]() ,点
,点![]() 到底面
到底面![]() 的距离为
的距离为![]() ,求出底面积,利用棱锥的体积公式可求得三棱椎
,求出底面积,利用棱锥的体积公式可求得三棱椎![]() 的体积.
的体积.
试题解析:(1)证明:如图,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,由底面
,由底面![]() 为菱形,可知点
为菱形,可知点![]() 为
为![]() 的中点,
的中点,
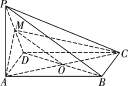
又∵![]() 为
为![]() 中点,
中点,
∴![]() 为
为![]() 的中位线,
的中位线,
∴![]() .
.
又∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)解:∵![]() 底面
底面![]() ,底面
,底面![]() 为菱形,
为菱形, ![]() ,∴
,∴![]() ,
,
又易得![]() ,
,
∴![]() ,
,
∵![]() ,得
,得![]() ,
,
∴点![]() 到底面
到底面![]() 的距离为
的距离为![]() ,
,
∴![]() .
.
【方法点晴】本题主要考查线面平行的判定定理、棱锥的体积公式,属于难题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:小学数学 来源: 题型:
【题目】小红、小明、小强、小方、小丽、小云的体重分别是:
32kg 40kg 37kg 34kg 36kg 37kg
(1)算出他们的平均体重。
(2)与平均体重相比,小红轻4kg,小明________,小强________,小方________小丽________,小云________。
(3)加果以平均体重为标准记为0千克,那么这6名同学的体重分别记作:
姓名 | 小红 | 小明 | 小强 | 小方 | 小丽 | 小云 |
体重(千克) | -4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com