
��������3���߳ʰ뻷�����������������������ʸ����������Ϸ��������������㻯կ���������������ڹ滮��Ψһһ���иܵ���·��ȫ��39.9ǧ�ף�39.9ǧ���ÿ�ѧ��������ʾΪ��������
A. 39.9��103�� B. 3.99��103�� C. 39.9��104�� D. 3.99��104��
D ��������39.9ǧ��=39000��=3.99��104�ף� ��ѡ��D.
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��������2017���п���ѧ��ģ�Ծ� ���ͣ������
��ͼ1����ƽ��ֱ������ϵ�У�������y=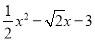 ��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C�������ߵĶ���Ϊ��D������B��BC�Ĵ��ߣ����Գ����ڵ�E��
��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y�ύ�ڵ�C�������ߵĶ���Ϊ��D������B��BC�Ĵ��ߣ����Գ����ڵ�E��
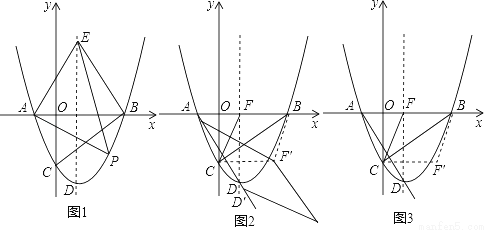
��1����֤����E���D����x��Գƣ�
��2����PΪ���������ڵ��������ϵ�һ���㣬����PAE��������ʱ���ڶԳ�������һ��M����y������һ��N��ʹ��OM+MN+NP��С�����ʱ��M�����꼰OM+MN+NP����Сֵ��
��3����ͼ2��ƽ�������ߣ�ʹ�����ߵĶ���D������AD���ƶ�����Dƽ�ƺ�Ķ�Ӧ��ΪD�䣬��A�Ķ�Ӧ��A�䣬�������ߵĶԳ�����x�ύ�ڵ�F������FBC��BC���ۣ�ʹ��F���ڵ�F�䴦����ƽ������һ��G������F�䡢G��D�䡢A��Ϊ������ı���Ϊ���Σ���ƽ�Ƶľ��룮
��1��֤������������2������3���� �� �������������������1���������A��B��C��D�����꣬�ٸ��ݡ�EFB�ס�BOC��Ӧ�߳ɱ����ó����̣��Ƴ�EF�ij��ȣ������E�����꼴�ɽ�����⣻ ��2������P��PQ��y�ᣬ��ֱ��AE�ڵ�Q������ ���κ��������ö��κ��������������P�����꣬����O���ڶԳ���ĶԳƵ�O�䣬����P����Y��ĶԳƵ�P�䣬����O��P�䣬�ֱԳ��ᡢy���ڵ�M��N����ʱM...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ�������꼶��̰���ѧ�Ծ���A���� ���ͣ���ѡ��
��֪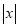 ��3��
��3�� 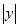 ��4����x��y����2x��y��ֵΪ��������
��4����x��y����2x��y��ֵΪ��������
A. ��2 B. ��2 C. ��10 D. ��2��10
D �����������������������֪x=��3��y=��4��������x��y�����x=3��y=-4��x=-3��y=-4�����2x-y=10��2x-y=-2. ��ѡD�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ�������꼶��̰���ѧ�Ծ���B���� ���ͣ������
����Ȼ�������¹������У�
������2�ڵڶ��е�һ�У����������ԣ�2��1����Ӧ����5�루1��3����Ӧ����14�루3��4����Ӧ��������һ���ɣ���2015��Ӧ����������Ϊ ��
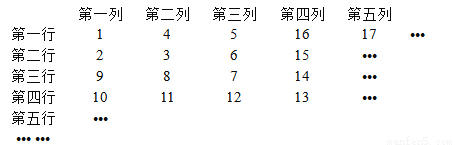
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ�������꼶��̰���ѧ�Ծ���B���� ���ͣ���ѡ��
��ͼ����֪l1��l2��AB��CD��CE��l2��FG��l2������˵��������ǣ�������
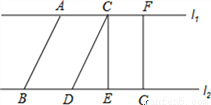
A. l1��l2֮��ľ������߶�FG�ij���
B. CE=FG
C. �߶�CD�ij��Ⱦ���l1��l2����ƽ����ľ���
D. AC=BD
C ���������١�FG��l2��AB��CD�� ��l1��l2֮��ľ������߶�FG�ij��ȣ� �ڡ�l1��l2��CE��l2�ڵ�E��FG��l2�ڵ�G�� ���ı���CEGF��ƽ���ı��Σ� ��CE=FG�� �ۡ�l1��l2��AB��CD�� ���ı���ABDC��ƽ���ı��Σ� ��AC=BD. �ۺ������ɵã�ABDѡ��Ľ���������ģ����ų�. ��ѡC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�갲��ʡ�Ϸ��и�������ѧУ�п���ѧģ���Ծ� ���ͣ������
��ͼ,������y=ax2+bx+c�Ķ���ΪM����2,��4������x�ύ��A��B����,��A����6,0������y�ύ�ڵ�C��
��1���������ߵĺ�������ʽ��
��2�����ABC�������
��3���ܷ��������ߵ�������ͼ�����ҵ�һ��P,ʹ��APC������������,�������P�����ꣻ�����ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�갲��ʡ�Ϸ��и�������ѧУ�п���ѧģ���Ծ� ���ͣ������
���㣺sin60��+|��5|��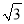 (4015����)0+(��1)2017+(
(4015����)0+(��1)2017+(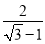 )��1��
)��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ƽ�30��ϵ�� ���꼶��ѧ С����÷� ���ͣ������
��ABC�У���A=30�㣬����B=________ ʱ����ABC�ǵ��������Σ�
75���30���120�� ���������������������AΪ���ǵ���30��ʱ���ɵõǡ�B=��180��-30�㣩=75�㣬��ABC�ǵ��������Σ�����A=��B=30��ʱ����ABC�ǵ��������Σ�����A=��C=30��ʱ�����B=120�㣬��ABC�ǵ��������Σ��ʴ�Ϊ��75���30���120�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ�������꼶��ʦ�����ѧ�Ծ���C���� ���ͣ���ѡ��
ƽ���������ཻ��6��ֱ�ߣ��佻���������Ϊm�������Ϊn������m��n����( )
A. 12 B. 16 C. 20 D. ���϶�����
B ����������������ɵã�6��ֱ���ཻ��һ��ʱ�������٣���ʱ����Ϊ1������m=1�� ������ֱ���ཻ������һ������ʱ������࣬ ����������ֱ�߲���ͬһ�㣬 ���ʱ����Ϊ��6����6-1����2=15����n=15�� ��m+n=16�� ��ѡB���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com