
�Ķ�����Ľ����̣���y2��4y��8����Сֵ��
��������
y2��4y��8��y2��4y��4��4��(y+2)2+4��4����(y��2)2��0��(y��2)2����СֵΪ0����y2��4y��8����СֵΪ4.
��������Ľ����̣���m2��m��4����Сֵ��4��x2��2x�����ֵ.
m2+m+4����Сֵ�ǣ����ֵ��5. ����������������1������ʽ�䷽������ȫƽ��ʽ����ڵ���0�����������Сֵ����2������ʽ�䷽������ȫƽ��ʽ����ڵ���0������������ֵ�� ��������� �������� ��1��m2+m+4=(m+)2+���ߣ�m+��2��0�� ��(m+)2+�ݣ���m2+m+4����Сֵ�ǣ� ���ߡ�0�����5�������ֵ��5. ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�㶫ʡ�������п���ѧģ���Ծ������� ���ͣ���ѡ��
|��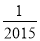 |���෴���ǣ�������
|���෴���ǣ�������
A. 2015 B. ��2015 C. 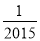 D. ��
D. ��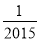
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�����з���2017-2018ѧ����꼶��ѧ�ڵڶ����¿���ѧ�Ծ� ���ͣ���ѡ��
С����֪��ѧУ��˵ĸ߶ȣ�����������ϵ����Ӵ������滹��1m�����������ӵ��¶�����5m�����¶˸պýӴ����棬����˵ĸ��ǣ��� ����
A. 8m B. 10m C. 12m D. 14m
C �����������������������������˵ĸ�ABΪx�ף�������AC�ij�Ϊ��x+1���ף������ù��ɶ����������AB�ij�������˵ĸߣ� �������� ����ʾ��ͼ������ʾ�� ����˵ĸ�ABΪxm��������AC�ij�Ϊ��x+1��m�� ��Rt��ABC�У�AB2+BC2=AC2�� ��x2+52=��x+1��2�� ��ã�x=12�� ��AB=12m�� ����˵ĸ���12m�� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ16-17ѧ��ȵ�һѧ�����꼶��ѧ��ĩ���Ծ� ���ͣ���ѡ��
��ͼ��һ��������ֽ�е�չ��ͼ��ÿ�����ڶ���ע����ĸ�����֣�����a��չ��ǰ���Ե���������ǣ���
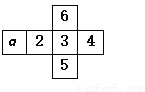
A. 2 B. 3 C. 4 D. 5
B ����������������ƽ��ͼ�ε��۵�������ͼ�εı���չ��ͼ���ص���⣮ ��𣺡������� �������ƽ��չ��ͼ�У��������ص���֮��һ�����һ�������Σ�������a��չ��ǰ���Ե����������3�� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ16-17ѧ��ȵ�һѧ�����꼶��ѧ��ĩ���Ծ� ���ͣ���ѡ��
��ʹ��ʽ(��4)��(��6)��2�����������Ӧ��������������(����)
A. �� B. �� C. �� D. ��
B ���������������㷨����㼴��ȷ����������ţ� �������� ��������ã���-4��-��-6��=-4+6=2�� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ũҵ��ѧ������ѧ2017-2018ѧ����꼶��ѧ�ڵ������¿���ѧ�Ծ� ���ͣ������
�������ж���ʽ��
��1��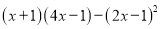
��2��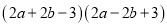
��3����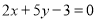 ����
����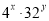 ��ֵ.
��ֵ.
��4���Ȼ�������ֵ��(2x��1)2��(3x+1)(3x��1)+5x(x��1)������x=��2��
��1�� ��2�� ��3��8;(4)20. ����������1�������ö���ʽ�ij˷����㣬��������ȫƽ����ʽ���㼴�ɣ���2������ƽ���ʽ���㼴�ɣ���3�������ݵij˷���ͬ�����ݵij˷�����������㼴�ɣ���4��ԭʽ����ƽ���ʽ����ȫƽ����ʽ���Լ�����ʽ���Զ���ʽ�������õ����������x��ֵ������㼴�����ֵ�� ��������� ��1��= �� ��2��ԭʽ= �� ��3����2x+5y=3, ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ũҵ��ѧ������ѧ2017-2018ѧ����꼶��ѧ�ڵ������¿���ѧ�Ծ� ���ͣ���ѡ��
��ͼ��Rt��ABC�У���C=90�㣬��B=45�㣬AD�ǡ�CAB��ƽ���ߣ�DE��AB��E��AB=a��CD=m����AC�ij�Ϊ
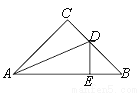
A. 2m B. a��m C. a D. a��m
B ������������AD�ǡ�CAB��ƽ���ߣ�DE��AB����C=90�㣬 ��CD=DE�� ��Rt��ACD��Rt��AED�У� �� ��Rt��ACD��Rt��AED��HL���� ��AC=AE�� �ߡ�B=45�㣬DE��AB�� ���BDE�ǵ���ֱ�������Σ� ��BE=DE=m�� ��AE=AB-BE=a-m�� ��AC=a-m�� ��ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʡ���������㷻��2017���п���ѧ��ģ�Ծ��������棩 ���ͣ������
��ͼ���ڡ�O�У�AC���ң�AD�����ߣ�CB��AD��B��CB���O�ཻ�ڵ�E������AE����AEƽ�֡�BAC��BE=1����CE=________��
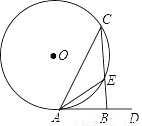
���𰸡�2
����������AD�����ߣ�  ��EAB=��C,
��EAB=��C,
��AE�ǽ�ƽ���ߣ�
��CAE=��EAB,
 ��CAE=��EAB=��C,
��CAE=��EAB=��C,
��CB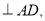
 ��C+��CAB=90�㣬
��C+��CAB=90�㣬
 3��C=90�㣬
3��C=90�㣬
 ��C=30��.
��C=30��.
�ʴ�Ϊ30��.
�����͡������
��������
19
��?ABCD�У��Ǿ��Σ�������AC����ABCΪֱ�������Σ���AB=4��AC=3����AD=________��
��5 ��������(1)��ͼ���ı�����ƽ���ı��Σ����ù��ɶ���֪��CD=AB,AD= (2) �ı�����ƽ���ı��Σ����ù��ɶ���֪��BC=AD=.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������2018ѧ������꼶���ϣ���ѧ��ĩ���Ծ� ���ͣ������
��ͼ��ʾ���߶�AB=8cm��EΪ�߶�AB���е㣬��CΪ�߶�EB��һ�㣬��EC=3cm����DΪ�߶�AC���е㣬���߶�DE�ij��ȣ�
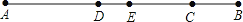
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com