
|﹣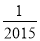 |的相反数是( )
|的相反数是( )
A. 2015 B. ﹣2015 C. 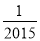 D. ﹣
D. ﹣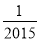
 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源:广东省2017年中考数学一模试卷 题型:单选题
如图,把一矩形纸片OABC放入平面直角坐标系xoy中,使OA,OC分别落在x轴、y轴上,现将纸片OABC沿OB折叠,折叠后点A落在点A'的位置,若OA=1,OB=2,则点A'的坐标为( )
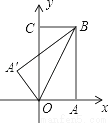
A. 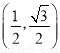 B.
B. 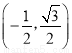 C.
C. 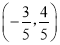 D. (
D. ( 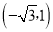
查看答案和解析>>
科目:初中数学 来源:江苏省徐州市丰县2018届九年级上学期第二次月考数学试卷 题型:填空题
一只不透明的袋子中装有1个蓝球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,记录颜色后放回、搅匀,再从中任意摸出1个球,则至少有1次摸到红球的概率__________
【解析】画树状图为: 共有9种等可能的结果数,其中至少有1次摸到红球的结果数为6, 所以任意摸出1个球, 至少有1次摸到红球的概率== . 故答案为.查看答案和解析>>
科目:初中数学 来源:2017广东省深圳市中考数学模拟试卷(三) 题型:填空题
如果水位升高3m时,水位变化记作+3m,那么水位下降5m时,水位变化记作: m.
-5. 【解析】试题解析:因为升高记为+,所以下降记为-,所以水位下降5m时水位变化记作-5m. 故答案为:-5.查看答案和解析>>
科目:初中数学 来源:2017广东省深圳市中考数学模拟试卷(三) 题型:单选题
12和20的公因数有( )
A. 2个 B. 3个 C. 4个 D. 5个
B 【解析】试题解析:20的因数有:1、2、4、5、10、20; 12的因数有:1、2、3、4、6、12; 20和12的公因数有:1、2、4,一共有3个; 故选B.查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西省七年级(下)第二次测验数学试卷 题型:解答题
已知(x2+px+8)(x2-3x+q)的展开式中不含x2和x3项,求p,q的值.
p=3,q=1. 【解析】试题分析:根据整式的乘法,化简完成后,根据不含项的系数为0求解即可. 试题解析:∵(x2+px+8)(x2﹣3x+q) =x4﹣3x3+qx2+px3﹣3px2+pqx+8x2﹣24x+8q =x4+(p﹣3)x3+(q﹣3p+8)x2+(pq﹣24)x+8q. ∵乘积中不含x2与x3项, ∴p﹣3=0,q﹣3p+8=0, ∴p=...查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西省七年级(下)第二次测验数学试卷 题型:填空题
钟面上3点40分时,时针与分针的夹角的度数是 度.
130° 【解析】 试题分析:每过一分钟,时针转动0.5°,分针转动6°.钟面上从4至8的角度为:30°×4=120°,时针与4之间的角度为:30°-0.5°×40=10°,则时针与分针的夹角为:120°+10°=130°.查看答案和解析>>
科目:初中数学 来源:江苏省徐州市丰县2017-2018学年八年级上学期第二次月考数学试卷 题型:解答题
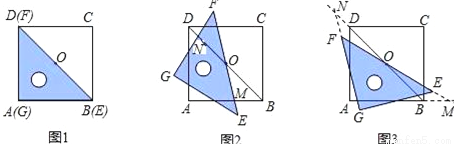
如图1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图2,当EF与AB相交于点M,GF与BD相交于点N时判断线段BM、FN的长度关系,并证明之;
(2)若三角尺GEF旋转到如图3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源:山西农业大学附属中学2017-2018学年八年级上学期第三次月考数学试卷 题型:解答题
阅读下面的解答过程,求y2+4y+8的最小值.
【解析】
y2+4y+8=y2+4y+4+4=(y+2)2+4≥4,∵(y+2)2≥0即(y+2)2的最小值为0,∴y2+4y+8的最小值为4.
仿照上面的解答过程,求m2+m+4的最小值和4﹣x2+2x的最大值.
m2+m+4的最小值是;最大值是5. 【解析】分析:(1)多项式配方后,根据完全平方式恒大于等于0,即可求出最小值;(2)多项式配方后,根据完全平方式恒大于等于0,即可求出最大值. 本题解析: 【解析】 (1)m2+m+4=(m+)2+,∵(m+)2≥0, ∴(m+)2+≥.则m2+m+4的最小值是; ,∵≤0,∴≤5,∴最大值是5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com