
若使等式(-4)□(-6)=2成立,则□中应填入的运算符号是( )
A. + B. - C. × D. ÷
B 【解析】利用运算法则计算即可确定出运算符号. 【解析】 根据题意得,(-4)-(-6)=-4+6=2, 故选B.科目:初中数学 来源:2017广东省深圳市中考数学模拟试卷(三) 题型:单选题
12和20的公因数有( )
A. 2个 B. 3个 C. 4个 D. 5个
B 【解析】试题解析:20的因数有:1、2、4、5、10、20; 12的因数有:1、2、3、4、6、12; 20和12的公因数有:1、2、4,一共有3个; 故选B.查看答案和解析>>
科目:初中数学 来源:江苏省徐州市丰县2017-2018学年八年级上学期第二次月考数学试卷 题型:填空题
在直角坐标系中,点A(-1,2)、B(4,3),点P(x,0)为x轴上的一个动点,则PA+PB最小时x的值为____________
1 【解析】【解析】 ∵点B(4,3),∴点B关于x轴的对称点的坐标为(4,-3),设直线A的解析式为y=kx+b,则 ,解得 ,∴y= -x+1, ∴P的坐标为(1,0),即x=1,故答案为,1.查看答案和解析>>
科目:初中数学 来源:安徽省16-17学年度第一学期七年级数学期末考试卷 题型:填空题
已知A,B两地相距450km,甲、乙两车分别从A,B两地同时出发,相向而行.已知甲车速度为120km/h,乙车速度为80km/h,经过t h两车相距50km,则t的值是_______________.
2或2.5 【解析】需要分两种情况. ①在相遇前相距50km,得方程(120+80)x=450-50. 解得x=2. ②在相遇后相距50km,得方程(120+80)x=450+50. 解得x=2.5. 故答案为2或2.5.查看答案和解析>>
科目:初中数学 来源:安徽省16-17学年度第一学期七年级数学期末考试卷 题型:单选题
有理数a,b,c在数轴上对应的点如图所示,那么( )
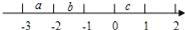
A. a+b+c>0 B. a+b+c<0 C. ab<ac D. ac>bc
B 【解析】由数轴可知-3<a<-2,-2<b<-1,0<c<1,所以A,C,D错误,B正确,故选B.查看答案和解析>>
科目:初中数学 来源:山西农业大学附属中学2017-2018学年八年级上学期第三次月考数学试卷 题型:解答题
阅读下面的解答过程,求y2+4y+8的最小值.
【解析】
y2+4y+8=y2+4y+4+4=(y+2)2+4≥4,∵(y+2)2≥0即(y+2)2的最小值为0,∴y2+4y+8的最小值为4.
仿照上面的解答过程,求m2+m+4的最小值和4﹣x2+2x的最大值.
m2+m+4的最小值是;最大值是5. 【解析】分析:(1)多项式配方后,根据完全平方式恒大于等于0,即可求出最小值;(2)多项式配方后,根据完全平方式恒大于等于0,即可求出最大值. 本题解析: 【解析】 (1)m2+m+4=(m+)2+,∵(m+)2≥0, ∴(m+)2+≥.则m2+m+4的最小值是; ,∵≤0,∴≤5,∴最大值是5.查看答案和解析>>
科目:初中数学 来源:山西农业大学附属中学2017-2018学年八年级上学期第三次月考数学试卷 题型:填空题
若点M(2,a+3)与点N(2,2a﹣15)关于x轴对称,则a2+3=_____________.
19 【解析】试题分析:根据纵坐标互为相反数列式求得a的值,代入所给代数式求值即可. 试题解析:∵点M(2,a+3)与点N(2,2a-15)关于x轴对称, ∴a+3+2a-15=0, 解得a=4, ∴a2+3=19.查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市香坊区2017年中考数学二模试卷(解析版) 题型:解答题
为了解青少年形体情况,现随机抽查了若干名初中学生坐姿、站姿、走姿的好坏情况(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:
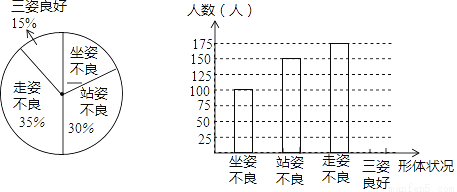
(1)求这次被抽查形体测评的学生一共有多少人?
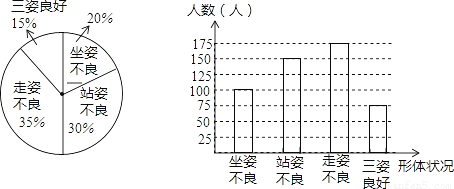
(2)求在被调查的学生中三姿良好的学生人数,并将条形统计图补充完整;
(3)若全市有5万名初中生,那么估计全市初中生中,坐姿和站姿不良的学生共有多少人?
【答案】(1)500名;(2)75名;(3)2.5万
【解析】试题分析:(1)用类型人数除以所占百分比就是总人数.(2)用总人数乘以15%.
(3) 坐姿和站姿不良的学生的学生的百分比乘以总人数.
试题解析:
(1)【解析】
100÷20%=500(名),
答:这次被抽查形体测评的学生一共是500名;
(2)【解析】
三姿良好的学生人数:500×15%=75名,
补全统计图如图所示;
(3)【解析】
5万×(20%+30%)=2.5万,
答:全市初中生中,坐姿和站姿不良的学生有2.5万人.
【题型】解答题
【结束】
24
如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.
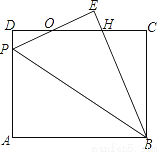
(1)求证:PE=DH;
(2)若AB=10,BC=8,求DP的长.
(1)见解析;(2). 【解析】试题分析:(1) 先证明△DOP≌△EOH,再利用等量代换得到PE=DH. (2) 设DP=x, Rt△BCH中,先用 x表示三角形三边,利用勾股定理列式解方程. 试题解析: (1)【解析】 证明:∵OD=OE,∠D=∠E=90°,∠DOP=∠EOH, ∴△DOP≌△EOH, ∴OP=OH, ∴PO+OE=OH+OD, ...查看答案和解析>>
科目:初中数学 来源:江西省抚州市2017-2018年上学期九年级数学期末试卷 题型:单选题
一次函数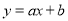 与二次函数
与二次函数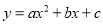 在同一直角坐标系中的图象可能是( )
在同一直角坐标系中的图象可能是( )
A. 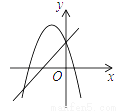 B.
B. 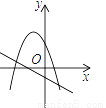
C. 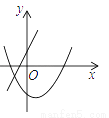 D.
D. 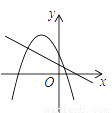
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com