练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

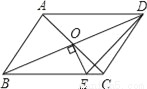
    如图，平行四边形ABCD的对角线交于点O，且AB≠AD，过O作OE⊥BD交BD于点E．若△CDE的周长为10，则平行四边形ABCD的周长为（　　）

    A. 10 B. 16 C. 18 D. 20

    D 【解析】∵四边形ABCD是平行四边形， ∴OB=OD，AB=CD，AD=BC， ∵OE⊥BD，∴BE=DE， ∵△CDE的周长为10， 即CD+DE+EC=10， ∴平行四边形ABCD的周长为：AB+BC+CD+AD=2(BC+CD)=2(BE+EC+CD)=2(DE+EC+CD)=2×10=20， 故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型：解答题

    在四边形ABCD中，对角线AC、BD相交于点O，设锐角∠AOB＝α，将△DOC按逆时针方向旋转得到△D′OC′（0°＜旋转角＜90°）连接AC′、BD′，AC′与BD′相交于点M．

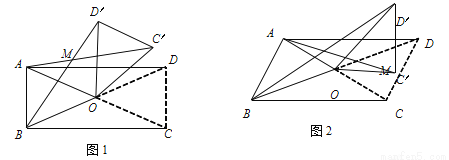
    (1)、当四边形ABCD为矩形时，如图1．求证：△AOC′≌△BOD′．

    (2)、当四边形ABCD为平行四边形时，设AC＝kBD，如图2．

    ①猜想此时△AOC′与△BOD′有何关系，证明你的猜想；

    ②探究AC′与BD′的数量关系以及∠AMB与α的大小关系，并给予证明．

    （1）见解析；（2）①、△BOD′∽△AOC′；（2）AC′=kBD′，∠AMB＝α． 【解析】试题分析：（1）证明：在矩形ABCD中，AC=BD，OA=OC=AC，OB=OD=BD，∴OA=OC=OB=OD，又∵OD=OD′，OC=OC′，∴OB=OD′=OA=OC′，∵∠D′OD=∠C′OC，∴180°﹣∠D′OD=180°﹣∠C′OC，∴∠BOD′=∠AOC′，∴在△BOD′和△AOC...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型：填空题

    ， ，若， ，则__________．

    【解析】由题意得： ∵， ． ∴， ∴．

    查看答案和解析>>

    科目：初中数学 来源：2017年内蒙古乌兰察布市中考数学一模试卷 题型：解答题

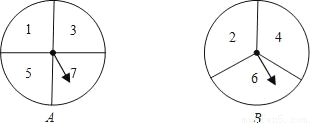
    如图，有A、B两个转盘，其中转盘A被分成4等份，转盘B被分成3等份，并在每一份内标上数字．现甲、乙两人同时各转动其中一个转盘，转盘停止后（当指针指在边界线上时视为无效，重转），若将A转盘指针指向的数字记为x，B转盘指针指向的数字记为y，从而确定点P的坐标为P（x，y）．

    （1）请用列表或画树状图的方法写出所有可能得到的点P的坐标；

    （2）计算点P在函数y=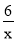图象上的概率．

    （1）列表见解析;（2）P=． 【解析】试题分析：（1）依据题意先用列表法或画树状图法分析所有等可能的出现结果，然后根据概率公式求出该事件的概率； （2）求点P落在反比例函数 图象上的概率，即求出即可． 试题解析：（1）列表法得： y x 2 4 6 1 （1，2） （1，4） （1，6） 3 （3，2） （3，...

    查看答案和解析>>

    科目：初中数学 来源：2017年内蒙古乌兰察布市中考数学一模试卷 题型：填空题

    化简：（+）÷=_____．

    【解析】试题解析：原式 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：2017年内蒙古乌兰察布市中考数学一模试卷 题型：单选题

    函数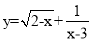中自变量x的取值范围是（　　）

    A. x≤2 B. x=3 C. x＜2且x≠3 D. x≤2且x≠3

    A 【解析】试题解析：根据题意得： 且x?3≠0， 解得： 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省徐州市中考数学模拟试卷（2） 题型：解答题

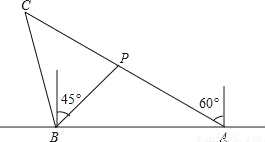
    如图，在一笔直的海岸线上有A，B两个观测站，A观测站在B观测站的正东方向，有一艘小船在点P处，从A处测得小船在北偏西60°方向，从B处测得小船在北偏东45°的方向，点P到点B的距离是3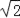千米．（注：结果有根号的保留根号）

    （1）求A，B两观测站之间的距离；

    （2）小船从点P处沿射线AP的方向以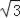千米/时的速度进行沿途考察，航行一段时间后到达点C处，此时，从B测得小船在北偏西15°方向，求小船沿途考察的时间．

    （1）(3+3)千米；（2）3小时． 【解析】试题分析：（1）过点P作PD⊥AB于点D.先解Rt△PBD，得到BD和PD的长，再解Rt△PAD，得到AD和AP的长，然后根据BD+AD=AB，即可求解； （2）过点B作BF⊥AC于点F.先解Rt△ABF，得出BF和AF的长，再解Rt△BCF，得出CF的长，可求PC=AF+CF-AP，从而求解． 试题解析：(1)如图，过点P作PD⊥AB于...

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省徐州市中考数学模拟试卷（2） 题型：单选题

    如图，在△ABC中，∠ACB=90º，AC=BC=1，E、F为线段AB上两动点，且∠ECF=45°，过点E、F分别作BC、AC的垂线相交于点M，垂足分别为H、G．现有以下结论：①AB=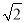；②当点E与点B重合时，MH=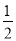；③AF+BE=EF；④MG•MH=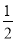，其中正确结论为（ ）

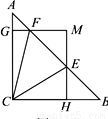
    A. ①②③ B. ①③④ C. ①②④ D. ①②③④

    C 【解析】试题解析：①由题意知，△ABC是等腰直角三角形， ∴AB=，故①正确； ②如图1，当点E与点B重合时，点H与点B重合， ∴MB⊥BC，∠MBC=90°， ∵MG⊥AC， ∴∠MGC=90°=∠C=∠MBC， ∴MG∥BC，四边形MGCB是矩形， ∴MH=MB=CG， ∵∠FCE=45°=∠ABC，∠A=∠ACF=45°， ∴C...

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷（十） 题型：填空题

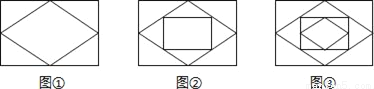
    已知：顺次连接矩形各边的中点，得到一个菱形，如图①；再顺次连接菱形各边的中点，得到一个新的矩形，如图②；然后顺次连接新的矩形各边的中点，得到一个新的菱形，如图③；如此反复操作下去，则第4个图形中直角三角形的个数有_____个；第2014个图形中直角三角形的个数有_____个．

    8 4028 【解析】图①、图②的直角三角形的个数相同，都是4，4=4×1， 图③、图④的直角三角形的个数相同，都是8，8=4×2， …… 图2013、图2014的直角三角形的个数相同，都是4×=4028． 故答案为：8；4028．

    查看答案和解析>>

    同步练习册答案