
估计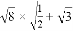 的运算结果应在( )
的运算结果应在( )
A. 1到2之间 B. 2到3之间 C. 3到4之间 D. 4到5之间
C 【解析】试题解析: = =, 的数值在1﹣2之间, 所以的数值在3﹣4之间. 故选C. 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:解答题
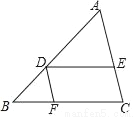
如图,在△ABC中,点D在边AB上,DE∥BC,DF∥AC,DE、DF分别交边AC、BC于点E、F,且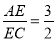 .
.
(1)求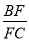 的值;
的值;
(2)联结EF,设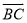 =
=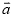 ,
, 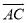 =
=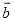 ,用含
,用含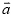 、
、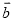 的式子表示
的式子表示 .
.
查看答案和解析>>
科目:初中数学 来源:北京市分校2017-2018学年度第一学期八年级数学期中试卷 题型:单选题
如图,已知△ABC的六个元素,则下列甲、乙、丙三个三角形中和△ABC全等的图形是( )

A. 甲 B. 乙 C. 丙 D. 乙与丙
D 【解析】【解析】 如图,在△ABC和△MNK中,∵∠B=∠N=50°,∠A=∠M=72°,BC=NK=a,∴△ABC≌△MNK(AAS); 在△ABC和△HIG中,∵AB=HI=c,∠B=∠I=50°,BC=IG=a,∴△ABC≌△HIG(SAS),∴甲、乙、丙三个三角形中和△ABC全等的图形是:乙或丙.故选D.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期中检测题 题型:填空题
如图所示,△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于点M,若EF=5,则CE2+CF2=___.
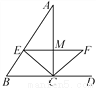
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期中检测题 题型:单选题
如图,△ABC中,AC的垂直平分线分别交AC、AB于点D、F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是( )
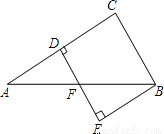
A.2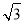 B.3
B.3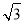 C.4 D.4
C.4 D.4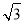
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省九年级数学科期末检测模拟试卷 题型:解答题
如图,把一张直角三角形卡片ABC放在每格宽度为12mm的横格纸中,三个顶点恰好都落在横格线上,已知∠BAC=90°,∠α=36°,求直角三角形卡片ABC的面积(精确到1mm).(参考数据:sin36°≈0.60,cos36°≈0.80,tan36°≈0.75)
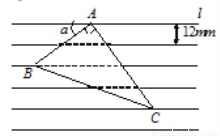
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省九年级数学科期末检测模拟试卷 题型:填空题
如图所示,圆盘被等分成八个全等的小扇形,并在上面依次标有数字1,2,3,4,5,6,7,8.自由转动转盘,当它停止转动时,指针指向的数字小于4的概率是______.
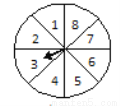
查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省济宁市嘉祥县九年级(上)月考数学试卷 题型:解答题
如图,△ABC是等边三角形,AO⊥BC,垂足为点O,⊙O与AC相切于点D,BE⊥AB交AC的延长线于点E,与⊙O相交于G,F两点.
(1)求证:AB与⊙O相切;
(2)若AB=4,求线段GF的长.
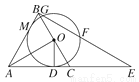
查看答案和解析>>
科目:初中数学 来源:山东省淄博市2018届九年级上学期期中考试数学试卷 题型:单选题
下列图案中属于旋转的是( )

A. A B. B C. C D. D
C 【解析】∵第(1)幅图案属于旋转;第(2)幅图案属于平移;第(3)幅图案属于旋转;第(4)幅图案属于旋转; ∴属于旋转的是图案是(1)、(3)、(4). 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com