
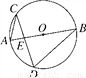
如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,BD.若AC=2,则cosD=________.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:单选题
下列图形中,是轴对称图形的有( )

A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴.由此可得,第1、2、3个图形是轴对称图形,第4个图形不是轴对称图形.故选C.查看答案和解析>>
科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
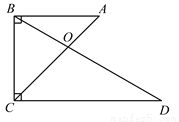
如图,∠ABC=∠BCD=90°,∠A=45°,∠D=30°,BC=1,AC,BD交于点O.求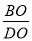 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:单选题
如图,AD∥BE∥CF,直线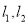 与这三条平行线分别交于点A,B,C和D,E,F.已知AB=1,BC=3,DE=2,则EF的长是( )
与这三条平行线分别交于点A,B,C和D,E,F.已知AB=1,BC=3,DE=2,则EF的长是( )
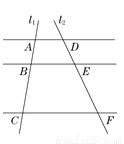
A. 4 B. 5 C. 6 D. 8
C 【解析】∵AD∥BE∥CF, ∴ , ∵AB=1,BC=3,DE=2, ∴ . 故选C.查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
如图,已知AB是⊙O的弦,P是AB上一点,AB=10,PA=4,OP=5,求⊙O的半径.
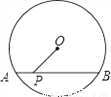
查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,⊙O是△ABC的外接圆,∠OCB=40°,则∠A的度数为( )

A. 60° B. 45° C. 50° D. 30°
D 【解析】如图,连接OB, 首先根据等腰三角形的性质得出∠OCB=∠OBC=40°,再根据圆周角定理,在同圆与等圆中同弧或等弧所对圆周角是圆心角的一半,即可得∠BOC=180°-40°-40°=100°,因此可得∠A=50°. 故选:D.查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:单选题
下列各图中,是中心对称图形的是( )

A. A B. B C. C D. D
A 【解析】试题分析:根据中心对称图形的定义:把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形进行解答。可知A选项是中心对称图形查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:填空题
已知△ABC∽△A1B1C1,△ABC的周长与△A1B1C1的周长的比值是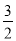 ,BE、B1E1分别是它 们对应边上的中线,且BE=6,则B1E1= .
,BE、B1E1分别是它 们对应边上的中线,且BE=6,则B1E1= .
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:填空题
若二次根式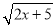 在实数范围内有意义,则x的取值范围是___________.
在实数范围内有意义,则x的取值范围是___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com